2.5D IP Forward Simulation - SimPEG User Tutorials

Keywords: Induced polarization, 2.5D forward simulation, apparent chargeability, tree mesh.

Summary: Here, we use the simpeg.electromagnetics.static.induced_polarization module to simulate 2.5D DC induced polarization (IP) data on a tree mesh. This approach is ideal when the local geology doesn’t change along the strike direction, as we can leverage the symmetry of the problem to reduce computational cost.

Because the same survey geometry, mesh and topography that are used to simulate DC resistivity data are used simulate IP data, almost all of the fundamental functionality used in this tutorial is described in detail in the 2.5D Forward Simulation of DC Resistivity Data tutorial. In this tutorial, we focus primarily on functionality related to the simulation of IP data. More specifically, we discuss:

Defining the chargeability model
How to simulate IP data
Units of the apparent chargeability model and predicted data

Import Modules¶

Here, we import all of the functionality required to run the notebook for the tutorial exercise. All of the functionality specific to IP is imported from simpeg.electromagnetics.static.induced_polarization. We also import some useful utility functions from simpeg.utils. To simulate DC and IP data, we need to define our problem geometry on a numerical grid (or mesh). To generate the mesh, we used the discretize package.

# SimPEG functionality
from simpeg.electromagnetics.static import induced_polarization as ip
from simpeg.utils import model_builder
from simpeg.utils.io_utils.io_utils_electromagnetics import write_dcip2d_ubc
from simpeg import maps, data
from simpeg.electromagnetics.static.utils.static_utils import (
    generate_dcip_sources_line,
    pseudo_locations,
    plot_pseudosection,
)

# discretize functionality
from discretize import TreeMesh
from discretize.utils import active_from_xyz

# Common Python functionality
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm, Normalize

mpl.rcParams.update({"font.size": 14})

write_output = False  # Optional

Define the Topography¶

True surface topography is defined as an (N, 3) numpy.ndarray. For use in a 2.5D simulation however, topography is defined as an (N, 2) numpy.ndarray, where the first coordinate represent along-line position and the second coordinate represents the vertical position. Here, we define the 2D topography used for the 2.5D simulation.

# Along-line locations
x_topo = np.linspace(-2000, 2000, 401)

# Elevation as a function of along-line location
T = 800.0
z_topo = 20.0 * np.sin(2 * np.pi * x_topo / T) + 140.0
z_topo[x_topo < -3 * T / 4] = 160.0
z_topo[x_topo > 3 * T / 4] = 120.0
z_topo += 50.0 * (1.0 + np.tanh(-3 * (x_topo + 1200.0) / T))
z_topo -= 50.0 * (1.0 + np.tanh(3 * (x_topo - 1200.0) / T))

# Define full 2D topography
topo_2d = np.c_[x_topo, z_topo]

# Plot 2D topography
fig = plt.figure(figsize=(10, 2))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(x_topo, z_topo, color="b", linewidth=2)
ax.set_xlabel("x (m)", labelpad=5)
ax.set_ylabel("z (m)", labelpad=5)
ax.grid(True)
ax.set_title("Topography (Exaggerated z-axis)", fontsize=16, pad=10)
plt.show(fig)

Define the IP Survey¶

A full description of elements required to define DC and IP surveys was presented in the 2.5D Forward Simulation of DC Resistivity Data tutorial. Here, we take the same approach. The only difference is that our receivers are defined to measure apparent chargeabilities. Because SimPEG uses a linearized formulation for simulating IP data; see Simulation2DCellCentered or Simulation2DNodal, the units of the apparent chargeability data are the same as the units chosen to represent the subsurface chargeabilities.

The survey line is an 800 m long EW dipole-dipole line with an electrode spacing of 40 m. There is a maximum of 10 potential electrodes per current electrode.

# Define survey line parameters
survey_type = "dipole-dipole"
dimension_type = "2D"
data_type = "apparent_chargeability"
end_locations = np.r_[-400.0, 400.0]
station_separation = 40.0
num_rx_per_src = 10

ip_source_list = generate_dcip_sources_line(
    survey_type,
    data_type,
    dimension_type,
    end_locations,
    topo_2d,
    num_rx_per_src,
    station_separation,
)

ip_survey = ip.survey.Survey(ip_source_list)

pseudo_locations_xz = pseudo_locations(ip_survey)
fig = plt.figure(figsize=(8, 2.75))
ax = fig.add_axes([0.1, 0.1, 0.85, 0.8])
ax.scatter(pseudo_locations_xz[:, 0], pseudo_locations_xz[:, -1], 8, "r")
ax.set_xlabel("x (m)")
ax.set_ylabel("z (m)")
ax.set_title("Pseudo-locations")
plt.show()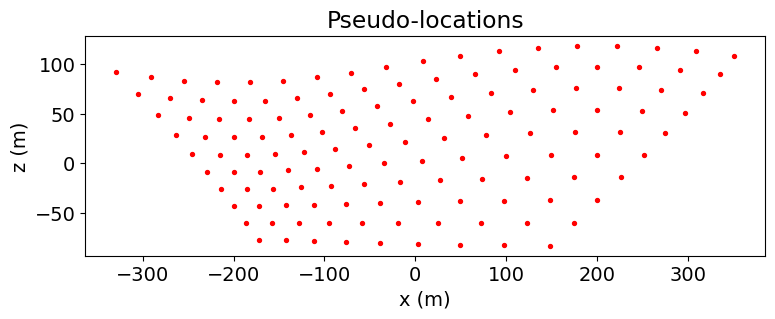

Design a (Tree) Mesh¶

Here, we generate a tree mesh based on the survey geometry. The best-practice approach for generating meshes for DC/IP simulations is provided in the 2.5D Forward Simulation of DC Resistivity Data tutorial.

dh = 4  # base cell width
dom_width_x = 3200.0  # domain width x
dom_width_z = 2400.0  # domain width z
nbcx = 2 ** int(np.round(np.log(dom_width_x / dh) / np.log(2.0)))  # num. base cells x
nbcz = 2 ** int(np.round(np.log(dom_width_z / dh) / np.log(2.0)))  # num. base cells z

# Define the base mesh with top at z = 0 m.
hx = [(dh, nbcx)]
hz = [(dh, nbcz)]
mesh = TreeMesh([hx, hz], x0="CN", diagonal_balance=True)

# Shift top to maximum topography
mesh.origin = mesh.origin + np.r_[0.0, z_topo.max()]

# Mesh refinement based on topography
mesh.refine_surface(
    topo_2d,
    padding_cells_by_level=[0, 0, 4, 4],
    finalize=False,
)

# Extract unique electrode locations.
unique_locations = ip_survey.unique_electrode_locations

# Mesh refinement near electrodes.
mesh.refine_points(
    unique_locations, padding_cells_by_level=[8, 12, 6, 6], finalize=False
)

mesh.finalize()

Define the Active Cells¶

Use the active_from_xyz utility function to obtain the indices of the active mesh cells from topography (e.g. cells below surface).

# Indices of the active mesh cells from topography (e.g. cells below surface)
active_cells = active_from_xyz(mesh, topo_2d)

# number of active cells
n_active = np.sum(active_cells)

Define the Background Conductivity/Resistivity¶

In order to simulate IP data, we require the background conductivity/resistivity defined on the entire mesh. You can generate this directly, or apply the appropriate mapping to a different parameterization of the conductivity/resistivity.

For the tutorial, we generate the conductivity model that was used for the 2.5D Forward Simulation of DC Resistivity Data tutorial; i.e. the electrical conductivities of all active cells. And so we must use the simpeg.maps.InjectActiveCells mapping to map from the model space to the conductivities on the entire mesh.

# Define electrical conductivities in S/m
air_conductivity = 1e-8
background_conductivity = 1e-2
conductor_conductivity = 1e-1
resistor_conductivity = 1e-3

# Define conductivity model
conductivity_model = background_conductivity * np.ones(n_active)

ind_conductor = model_builder.get_indices_sphere(
    np.r_[-120.0, 40.0], 60.0, mesh.cell_centers[active_cells, :]
)
conductivity_model[ind_conductor] = conductor_conductivity

ind_resistor = model_builder.get_indices_sphere(
    np.r_[120.0, 72.0], 60.0, mesh.cell_centers[active_cells, :]
)
conductivity_model[ind_resistor] = resistor_conductivity

# Mapping from conductivity model to mesh
conductivity_map = maps.InjectActiveCells(mesh, active_cells, air_conductivity)

# Mapping to neglect air cells when plotting
plotting_map = maps.InjectActiveCells(mesh, active_cells, np.nan)

fig = plt.figure(figsize=(9, 4))
norm = LogNorm(vmin=1e-3, vmax=1e-1)

ax1 = fig.add_axes([0.14, 0.17, 0.68, 0.7])
mesh.plot_image(
    plotting_map * conductivity_model,
    ax=ax1,
    grid=False,
    pcolor_opts={"norm": norm, "cmap": mpl.cm.RdYlBu_r},
)
ax1.set_xlim(-500, 500)
ax1.set_ylim(-300, 200)
ax1.set_title("Background Conductivity Model")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("z (m)")

ax2 = fig.add_axes([0.84, 0.17, 0.03, 0.7])
cbar = mpl.colorbar.ColorbarBase(
    ax2, norm=norm, orientation="vertical", cmap=mpl.cm.RdYlBu_r
)
cbar.set_label(r"$\sigma$ (S/m)", rotation=270, labelpad=15, size=12)

plt.show()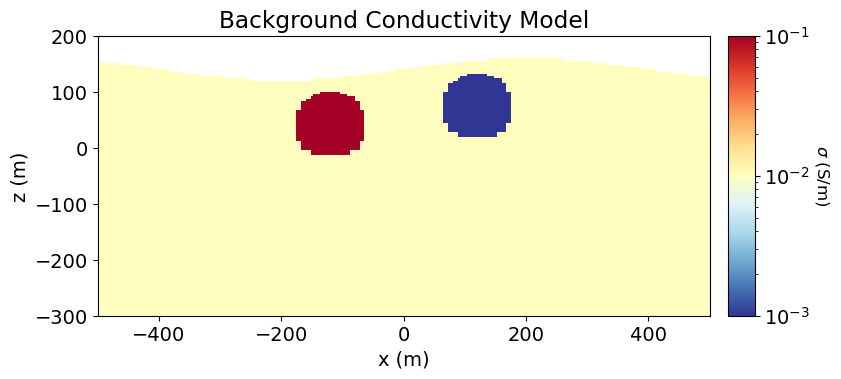

Define the Chargeability Model and Mapping¶

The model does not need to be synonymous with the physical property values. But it is common to define chargeability models as the chargeabilities for all subsurface (active) cells. So, what are the units?

SimPEG uses a linearized formulation for simulating IP data; see Simulation2DCellCentered or Simulation2DNodal. In this formulation, any standard definition of the chargeability can be used. And the resulting apparent chargeability data will be in terms of the same units; e.g. intrinsic chargeability (V/V or mV/V) or integrated chargeability (ms). If you are simulating secondary voltages, the chargeability model must represent intrinsic chargeabilities ( $0 \leq \eta \leq 1$ ) in V/V.

For this tutorial, we use the intrinsic chargeability in units V/V. Here, the conductive sphere is chargeable, but the resistive sphere and the host are not. Note that unlike DC resistivity, the physical property value defining air cells for IP simulation can be set to zero.

# Intrinsic chargeability in V/V (unitless).
air_chargeability = 0.0
background_chargeability = 0.0
sphere_chargeability = 1e-1

# Define chargeability model
chargeability_model = background_chargeability * np.ones(n_active)

ind_chargeable = model_builder.get_indices_sphere(
    np.r_[-120.0, 40.0], 60.0, mesh.cell_centers[active_cells, :]
)
chargeability_model[ind_chargeable] = sphere_chargeability

# Define mapping for chargeability
chargeability_map = maps.InjectActiveCells(mesh, active_cells, air_chargeability)

# Plot Chargeability Model
fig = plt.figure(figsize=(9, 4))

norm = Normalize(vmin=0.0, vmax=0.1)

ax1 = fig.add_axes([0.14, 0.17, 0.68, 0.7])
mesh.plot_image(
    plotting_map * chargeability_model,
    ax=ax1,
    grid=False,
    pcolor_opts={"cmap": mpl.cm.plasma, "norm": norm},
)
ax1.set_xlim(-500, 500)
ax1.set_ylim(-300, 200)
ax1.set_title("Intrinsic Chargeability")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("z (m)")

ax2 = fig.add_axes([0.84, 0.17, 0.03, 0.7])
cbar = mpl.colorbar.ColorbarBase(
    ax2, norm=norm, orientation="vertical", cmap=mpl.cm.plasma
)
cbar.set_label("Intrinsic Chargeability (V/V)", rotation=270, labelpad=15, size=12)

plt.show()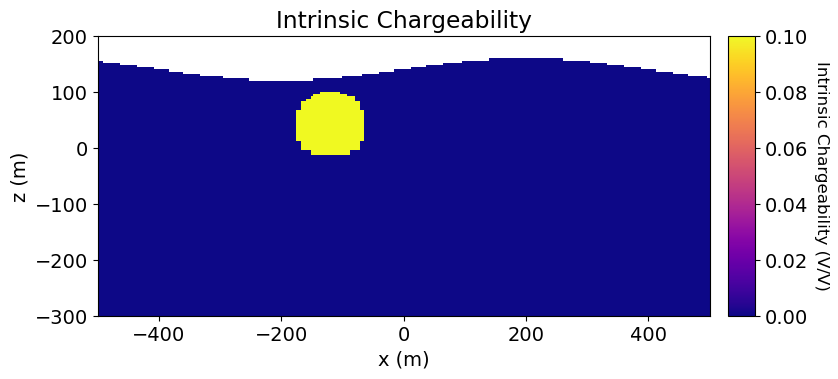

Project Electrodes to Discretized Topography¶

As explained in the 2.5D Forward Simulation of DC Resistivity Data tutorial, we use the drape_electrodes_on_topography method to project the electrodes to the discrete surface topography.

ip_survey.drape_electrodes_on_topography(mesh, active_cells, option="top")

Define the IP Simulation¶

There are two simulation classes which may be used to simulate 2.5D IP data:

Simulation2DNodel, which defines the discrete electric potentials on mesh nodes.
Simulation2DCellCentered, which defines the discrete electric potentials at cell centers.

For surface DC and IP data, the nodal formulation is more well-suited and will be used here. The cell-centered formulation works well for simulating borehole DC and IP data. To fully define the forward simulation, we need to connect the simulation object to:

the survey
the mesh
a background conductivity or resistivity model
the mapping from the chargeability model to the mesh

If working with electrical conductivity, use the sigma keyword argument to define the background conductivity on the entire mesh. If working with electrical resistivity, use the rho keyword argument to define the background resistivity on the entire mesh. The etaMap is used to define the mapping from the chargeability model to the chargeabilities on the entire mesh.

ip_simulation = ip.Simulation2DNodal(
    mesh,
    survey=ip_survey,
    etaMap=chargeability_map,
    sigma=conductivity_map * conductivity_model,
)

Simulate IP Data¶

dpred_ip = ip_simulation.dpred(chargeability_model)

/t40array/ssoler/miniforge3/envs/simpeg-user-tutorials/lib/python3.10/site-packages/simpeg/electromagnetics/static/resistivity/simulation_2d.py:756: RuntimeWarning: invalid value encountered in divide
  r_hat = r_vec / r[:, None]
/t40array/ssoler/miniforge3/envs/simpeg-user-tutorials/lib/python3.10/site-packages/simpeg/electromagnetics/static/resistivity/simulation_2d.py:783: RuntimeWarning: invalid value encountered in divide
  alpha[not_top] = (ky * k1e(ky * r) / k0e(ky * r) * r_dot_n)[not_top]
/t40array/ssoler/miniforge3/envs/simpeg-user-tutorials/lib/python3.10/site-packages/simpeg/simulation.py:197: DefaultSolverWarning: Using the default solver: Pardiso. 

If you would like to suppress this notification, add 
warnings.filterwarnings('ignore', simpeg.utils.solver_utils.DefaultSolverWarning)
 to your script.
  return get_default_solver(warn=True)

Plot IP Data in Pseudosection¶

Here we use the plot_pseudosection utility function to represent predicted data on pseudosection plots.

fig = plt.figure(figsize=(9, 4))

ax1 = fig.add_axes([0.1, 0.1, 0.7, 0.8])
cax1 = fig.add_axes([0.82, 0.1, 0.025, 0.8])
plot_pseudosection(
    ip_survey,
    dpred_ip,
    "contourf",
    ax=ax1,
    cax=cax1,
    scale="linear",
    cbar_label="V/V",
    mask_topography=True,
    contourf_opts={"levels": 20, "cmap": mpl.cm.plasma},
)
ax1.set_title("Apparent Chargeability (V/V)")

plt.show()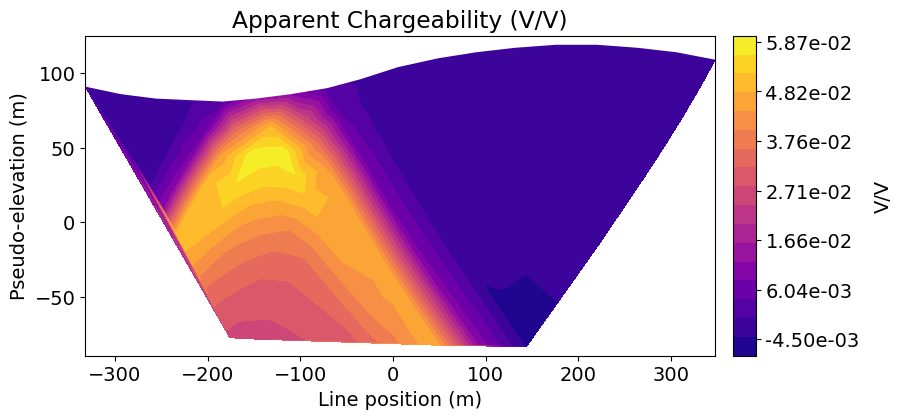

Optional: Write data and topography

if write_output:
    dir_path = os.path.sep.join([".", "fwd_ip_2d_outputs"]) + os.path.sep
    if not os.path.exists(dir_path):
        os.mkdir(dir_path)

    # Add 5% Gaussian noise to each datum
    rng = np.random.default_rng(seed=225)
    std = 5e-3 * np.ones_like(dpred_ip)
    ip_noise = rng.normal(scale=std, size=len(dpred_ip))
    dobs = dpred_ip + ip_noise

    # Create a survey with the original electrode locations
    # and not the shifted ones
    # Generate source list for DC survey line
    source_list = generate_dcip_sources_line(
        survey_type,
        data_type,
        dimension_type,
        end_locations,
        topo_2d,
        num_rx_per_src,
        station_separation,
    )
    survey_original = ip.survey.Survey(source_list)

    # Write out data at their original electrode locations (not shifted)
    data_obj = data.Data(survey_original, dobs=dobs, standard_deviation=std)
    fname = dir_path + "ip_data.obs"
    write_dcip2d_ubc(fname, data_obj, "apparent_chargeability", "dobs")

    fname = dir_path + "topo_2d.txt"
    np.savetxt(fname, topo_2d, fmt="%.4e")

SimPEG User Tutorials

Induced Polarization

SimPEG User Tutorials

3D IP Forward Simulation