3D IP Inversion

Keywords: induced polarization, 3D inversion, sparse norm, tree mesh.

Summary: Here we invert apparent chargeability data to recover the subsurface chargeability distribution on a tree mesh. We demonstrate two inversion approaches for recovering a chargeability model:

1. Weighted least-squares inversion
2. Iteratively re-weighted least-squares (IRLS) inversion

Almost all of the details of defining and carrying out weighted least-squares and iteratively weighted least squares inversion were covered in the 3D DC Resistivity Inversion tutorial. And functionality specific to defining the IP forward simulation was covered in the 3D IP Forward Simulation tutorial. As we will focus primarily on content specific to IP inversion, we strongly urge the reader to work through the aforementioned tutorials prior to working through this one.

Learning Objectives:

• Assigning appropriate uncertainties to IP data
• Designing a mesh for IP inversion
• Obtaining a background conductivity/resistivity model for the IP inversion
• Analyzing inversion results

Import Modules¶

Here, we import all of the functionality required to run the notebook for the tutorial exercise. All of the functionality specific to IP is imported from simpeg.electromagnetics.static.induced_polarization. We also import some useful utility functions from simpeg.utils. Classes required to define the data misfit, regularization, optimization, etc... are imported from elsewhere within SimPEG. We also import some useful utility functions from simpeg.utils. To generate the mesh used for the inversion, we use the discretize package.

Load and Plot Tutorial Data¶

For most geophysical inversion projects, a reasonable inversion result can be obtained so long as the practitioner has observed data, the survey geometry and topography. For this tutorial, the observed data and topography files are provided. Here, we download and import the observed data and topography into the SimPEG framework.

Load the Topography¶

For most geophysical inversion projects, a reasonable inversion result can be obtained so long as the practitioner has observed data, the survey geometry and topography. For this tutorial, the observed data and topography files are provided. Here, we download and import the observed data and topography into the SimPEG framework.

Load IP Data¶

Option A: DCIP3D formatted data

The read_dcip3d_ubc utility function can be used to load DC/IP data stored in a UBC-GIF formatted file. This function outputs a SimPEG Data object.

Option B: Load XYZ formatted data

For this tutorial, the observed data are organized within an XYZ formatted file. We can use the read_dcip_xyz utility function to load data in this format. This function outputs a SimPEG Data object. The data are apparent chargeabilities in V/V.

The dict_headers input argument can be used to import other data columns that are not required to define the SimPEG data object. In this case, we import a column that defines the survey line associated with each datum. We will use this to plot pseudosections for individual survey lines.

Plot Observed Data in 3D Pseudosection¶

Here we use the plot_3d_pseudosection utility function to represent the observed data in pseudosection. In this case, the apparent chargeabilities are represented in V/V.

In the case of secondary voltage data, you would need to convert the values to apparent chargeabilities. This accomplished by normalizing the secondary IP voltages by the DC voltages.

Plot Observed Data in 2D Pseudosection¶

As demonstrated in the 3D Forward Simulation tutorial, we can parse the 3D survey into a set of 2D survey lines if we know which survey line is associated with each datum. Then we can plot individual pseudosections for each survey line. We use the convert_survey_3d_to_2d_lines to generate the list of 2D surveys. And we use the plot_2d_pseudosection utility function to plot the pseudosection for the desired survey line.

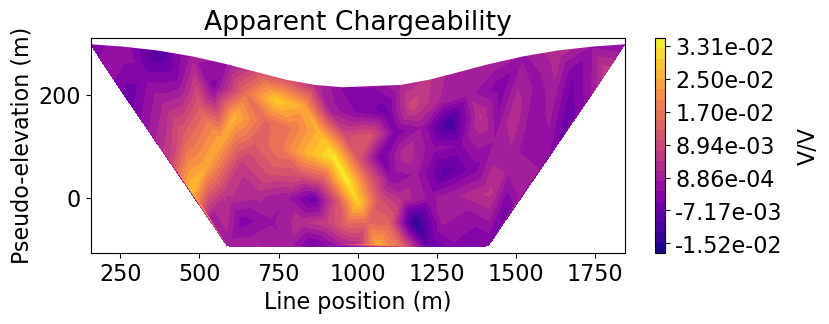
Assign Uncertainties¶

Inversion with SimPEG requires that we define the uncertainties on our data; that is, an estimate of the standard deviation of the noise on our data assuming it is uncorrelated Gaussian with zero mean. An online resource explaining uncertainties and their role in the inversion can be found here.

For secondary voltage data, we generally apply a percent uncertainty and a very small floor uncertainty to all data. Differences in electrode spacing and subsurface conductivity result in secondary voltage IP data that span many orders of magnitude. A percent uncertainty ensures all data are fit equally. Depending on the quality of the data, we may choose a percent uncertainty between 2% - 10%. The floor uncertainty ensures stability when there are zero-crossings or erroneously small voltages.

For apparent chargeability data, we generally apply a floor uncertainty to all data. This is because apparent chargeability data is obtained by normalizing the secondary voltage defining the IP signature by the DC voltage. This effectively removes the influence of electrode spacing on the amplitude of the datum. Here, we apply a floor uncertainty of 5e-3 V/V to all data.

Design a (Tree) Mesh¶

IP inversion is carried out on the same mesh that is used for DC resistivity inversion. Here, we reproduce the survey-based meshing approach that was used in the 3D Inversion of DC Resistivity Data tutorial. The best-practices for meshes design for DC/IP problems is provided in the 2.5D Forward Simulation of DC Resistivity Data tutorial. The same rules for defining appropriate meshes for 2.5D simulations and inversion apply to 3D simulations and inversion.

Tutorial mesh: Here, a minimum cell width of 25 m (or 1/4 the minimum electrode spacing) is used within our survey region. The largest electrode spacing was 1000 m, so a the padding was extended at least 3000 m from the survey region. Using the refine_surface method, we refine the tree mesh where there is significant topography. And using the refine_points methods, we refine based on electrodes locations. Visit the tree mesh API to see additional refinement methods.

Define the Active Cells¶

Use the active_from_xyz utility function to obtain the indices of the active mesh cells from topography (e.g. cells below surface).

Project Electrodes to Discretized Topography¶

Surface IP data will not be modeled accurately if the electrodes are modeled as living above or below the surface. It is especially problematic when electrodes are modeled as living in the air. Prior to inverting surface IP data, we must project the electrodes from their true elevation to the surface of the discretized topography. This is done using the drape_electrodes_on_topography method.

Define the Background Conductivity/Resistivity¶

In order to invert IP data, we require the background conductivity/resistivity defined on the entire mesh. In practice, a conductivity/resistivity model is recovered via inverting DC resistivity data; see the 3D Inversion of DC Resistivity Data tutorial. Since the conductivity/resistivity model greatly impacts the sensitivities for the IP problem, IP inversion is most successful when the recovered conductivity/resistivity model accurately characterizes the true subsurface distribution of electrical properties. For the tutorial, the true subsurface conductivity is used as the background conductivity for the IP inversion.

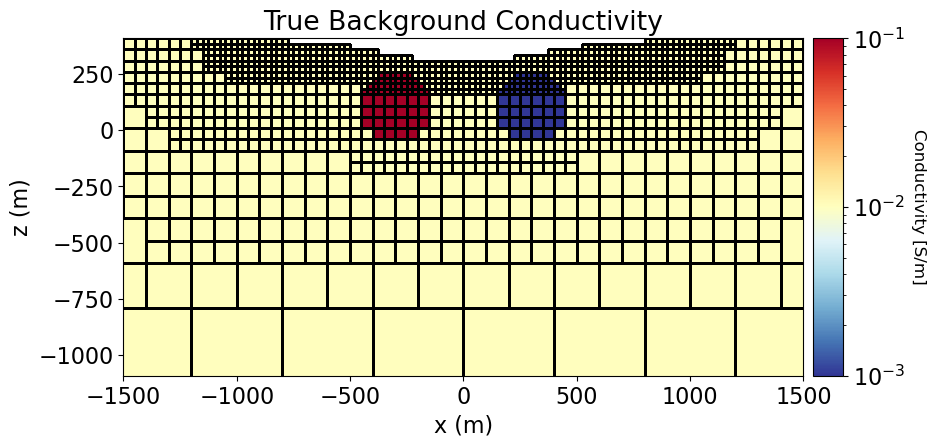
Mapping from the Model to the Mesh¶

In SimPEG, the term ‘model’ is not synonymous with the physical property values defined on the mesh. For whatever model we choose, we must define a mapping from the set of model parameters (a 1D numpy.ndarray) to the physical property values of all cells in the mesh. Mappings are created using the simpeg.maps module.

SimPEG uses a linearized formulation for simulating IP data; see Simulation2DCellCentered or Simulation2DNodal. In this formulation, any standard definition of the chargeability can be inverted. And the units of the recovered chargeability values is the same as the data units; e.g. intrinsic chargeability (V/V or mV/V) or integrated chargeability (ms). If you are inverting secondary voltages however, the chargeability model must represent intrinsic chargeabilities ($0 \leq \eta \leq 1$) in V/V.

In this tutorial, the model parameters are the subsurface chargeabilities ($0 \leq \eta \leq 1$) in V/V. We use the simpeg.maps.InjectActiveCells map to project the active cell chargeabilities to the entire mesh.

Starting/Reference Model for IP Inversion¶

Here, we would create starting and/or reference models for the IP inversion as well as the mapping from the model space to the active cells. Starting and reference models can be a constant background value or contain a-priori structures. Here, the starting model is the 1e-6 V/V. It should be noted that the starting model cannot be vector of zeros, otherwise the inversion will be unable to compute a gradient direction at the first iteration.

Define the Forward Simulation¶

A simulation object defining the forward problem is required in order to predict data and calculate misfits for recovered models. A comprehensive description of the simulation object for 3D IP was discussed in the 3D IP Forward Simulation tutorial. Here, we use the Simulation3DNodal simulation which solves for the electric potential on mesh nodes.

Since we are using a background conductivity model, we use sigma to define the background conductivity on the entire mesh. Because the IP problem has been linearized, we store the sensitivities for the inversion using storeJ.

Define the Data Misfit¶

To understand the role of the data misfit in the inversion, please visit this online resource. Here, we use the L2DataMisfit class to define the data misfit. In this case, the data misfit is the L2 norm of the weighted residual between the observed data and the data predicted for a given model. When instantiating the data misfit object within SimPEG, we must assign an appropriate data object and simulation object as properties.

Define the Regularization¶

To understand the role of the regularization in the inversion, please visit this online resource. Here, we use the WeightedLeastSquares regularization class to constrain the inversion result. Length scales along x, y and z are used to balance the smallness and smoothness terms. And the reference model is only applied to the smallness term; which is redundant for the tutorial example since we have set the reference model to an array of zeros.

By default, the regularization acts on the model parameters; which in the case are the log-conductivities of the active cells. So we need to specify which cells are active in the regularization. And if we wanted to apply the regularization to a function of the model parameters, we would need to set an approprate mapping object using the mapping keyword argument.

Define the Optimization Algorithm¶

Here, we use the ProjectedGNCG class to solve the optimization problem using projected Gauss-Newton with conjugate gradietn solver. Reasonable default values have generally been set for the properties of each optimization class. However, the user may choose to set custom values; e.g. the accuracy tolerance for the conjugate gradient solver or the number of line searches. Here, the lower property is set to 0 to ensure recovered chargeability values are positive.

Define the Inverse Problem¶

We use the BaseInvProblem class to fully define the inverse problem that is solved at each beta (trade-off parameter) iteration. The inverse problem requires appropriate data misfit, regularization and optimization objects.

Provide Inversion Directives¶

Directives represent operations that are applied while the inversion is running. Here, we apply common directives for weighted least-squares inversion of IP data and describe their roles. These are:

• UpdateSensitivityWeights: Apply sensitivity weighting to counteract the natural tendency of IP inversion to place materials near the electrodes. Since the IP problem has been linearized, we do not need to update the sensitivities and we set every_iteration=False. For IP inversion, we do not want to use the entire dynamic range of the sensitivities to generate our weighting. So we generally set threshold_value to a value betwewen 1e-4 and 1e-1.

• UpdatePreconditioner: Apply Jacobi preconditioner when solving optimization problem to reduce the number of conjugate gradient iterations. We set update_every_iteration=False because the ideal preconditioner because the forward problem and regularization are not model-dependent.

• BetaEstimate_ByEig: Compute and set starting trade-off parameter (beta) based on largest eigenvalues.

• BetaSchedule: Size reduction of the trade-off parameter at every beta iteration, and the number of Gauss-Newton iterations for each beta. In general, a coolingFactor between 1.5 and 2.5, and coolingRate of 2 or 3 works well for DC resistivity inversion. Cooling beta too quickly will result in portions of the model getting trapped in local minima. And we will not be finding the solution that minimizes the optimization problem if the cooling rate is too small.

• TargetMisfit: Terminates the inversion when the data misfit equals the target misfit. A chifact=1 terminates the inversion when the data misfit equals the number of data.

The directive objects are organized in a list. Upon starting the inversion or updating the recovered model at each iteration, the inversion will call each directive within the list in order. The order of the directives matters, and SimPEG will throw an error if directives are organized into an improper order. Some directives, like the BetaEstimate_ByEig are only used when starting the inversion. Other directives, like UpdatePreconditionner, are used whenever the model is updated.

Define and Run the Inversion¶

We define the inversion using the BaseInversion class. The inversion class must be instantiated with an appropriate inverse problem object and directives list. The run method, along with a starting model, is respondible for running the inversion. The output is a 1D numpy.ndarray containing the recovered model parameters

Analyze Inversion Outputs¶

Plot Normalized Data Misfit in 3D Pseudosection¶

To see how well the recovered model reproduces the observed data, it is a good idea to compare the predicted and observed data. Here, we plot the normalized data misfit to determine whether the observed data are fit evenly. Correlated signatures in the normalized data misfits indicate we are overfitting/underfitting certain data. And that we must modify our uncertainties and re-run the inversion.

Plot 2D Pseudsections for Individual Survey Lines¶

For large datasets comprised of many survey lines, interpretation can be challenging if we plot every datum. Here, we plot the observed data, predicted data and data misfit for a specified survey line.

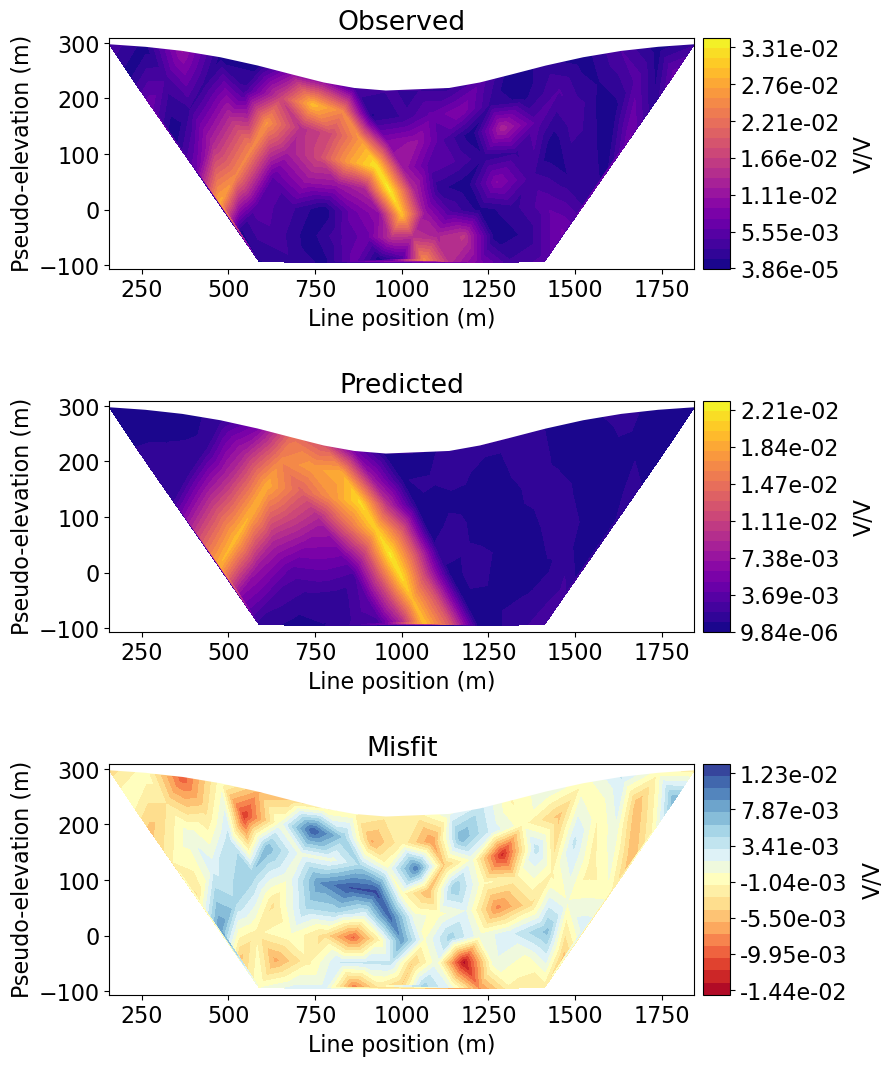
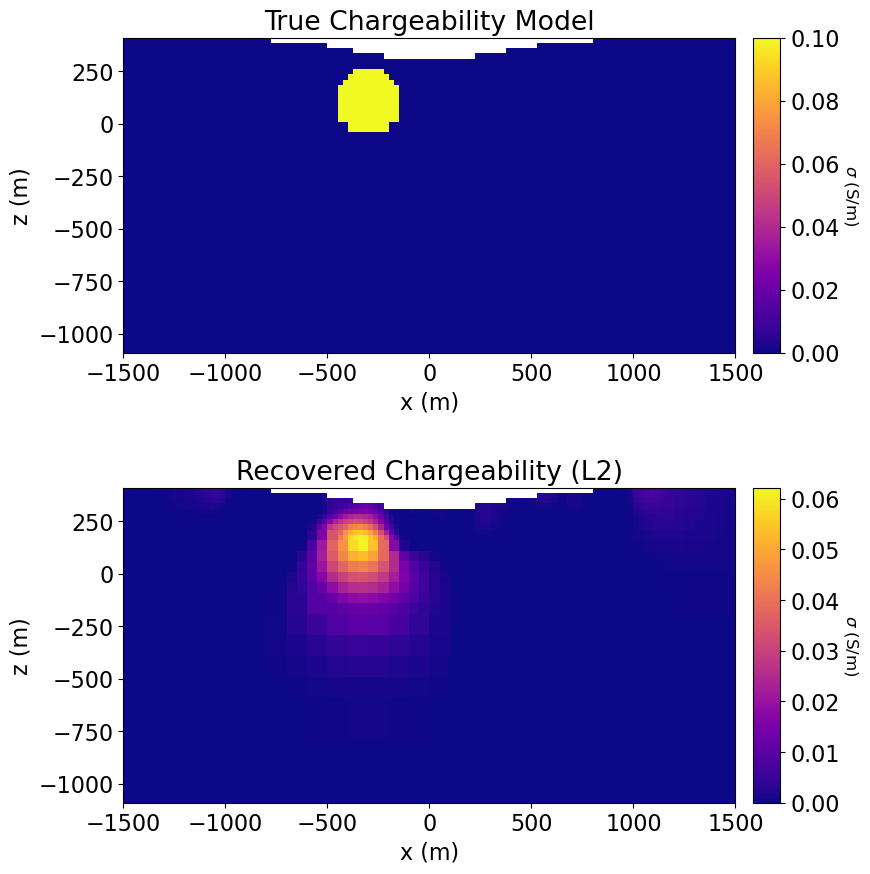
Plot True and Recovered Chargeability Models¶