3D Forward Simulation of Gravity Gradiometry Data

Keywords: gravity anomaly, forward simulation, integral formulation, tree mesh.

Summary: Here we use the module simpeg.potential_fields.gravity to simulate gravity gradiometry data for a synthetic density contrast model. We use the 3D integral formulation and carry out the forward simulation on a tree mesh.

Learning Objectives:

How to simulate gravity data for 3D structures with SimPEG.
How to create gravity gradiometry surveys and manage multiple data components.
How to design a tree mesh for gravity simulation (integral solution).
How to predict gravity gradiometry data for a density contrast model.
How to include surface topography in the forward simulation.
What are the units of the density contrast model and resulting data.

Import Modules¶

Here, we import all of the functionality required to run the notebook for the tutorial exercise. All of the functionality specific to simulating gravity data are imported from simpeg.potential_fields.gravity. We also import some useful utility functions from SimPEG. To simulate gravity data, we need to define our problem geometry on a numerical grid (or mesh). To generate the mesh, we used the discretize package.

# SimPEG functionality
from simpeg.potential_fields import gravity
from simpeg.utils import plot2Ddata, model_builder
from simpeg import maps

# discretize functionality
from discretize import TreeMesh
from discretize.utils import mkvc, active_from_xyz

# Common Python functionality
import numpy as np
from scipy.interpolate import LinearNDInterpolator
import matplotlib as mpl

mpl.rcParams.update({"font.size": 14})
import matplotlib.pyplot as plt

save_output = False  # Optional

Define the Topography¶

Surface topography is defined as an (N, 3) numpy.ndarray for 3D simulations. Here, we create basic topography for the forward simulation. For user-specific simulations, you may load topography from an XYZ file.

[x_topo, y_topo] = np.meshgrid(np.linspace(-200, 200, 41), np.linspace(-200, 200, 41))
rng = np.random.default_rng(seed=737)
z_topo = (
    -15 * np.exp(-(x_topo**2 + y_topo**2) / 80**2)
    + 100.0
    + rng.uniform(low=0.0, high=0.5, size=x_topo.shape)
)

fig = plt.figure(figsize=(6, 6))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8], projection="3d")
ax.set_zlim([z_topo.max() - 40, z_topo.max()])
ax.plot_surface(x_topo, y_topo, z_topo, color="r", edgecolor="k", linewidth=0.5)
ax.set_box_aspect(aspect=None, zoom=0.85)
ax.set_xlabel("X (m)", labelpad=10)
ax.set_ylabel("Y (m)", labelpad=10)
ax.set_zlabel("Z (m)", labelpad=10)
ax.set_title("Topography (Exaggerated z-axis)", fontsize=16, pad=-20)
ax.view_init(elev=20.0)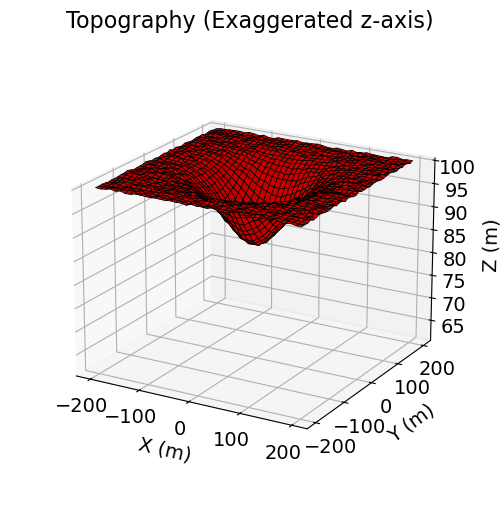

x_topo, y_topo, z_topo = mkvc(x_topo), mkvc(y_topo), mkvc(z_topo)
topo_xyz = np.c_[x_topo, y_topo, z_topo]

Define the Survey¶

Surveys within SimPEG generally require the user to create and connect three types of objects:

receivers: which define the locations of field measurements and type of data being measured.
sources: the passive or active sources responsible for generating geophysical responses, and their associated receivers.
survey: the object which stores and organizes all of the sources and receivers.

Here, we define the survey that will be used for the forward simulation. Gravity surveys are simple to create. The user only needs an (N, 3) numpy.ndarray to define the xyz locations of the observation locations, and a list of field components which are to be measured. For the tutorial simulation, the receivers are located 5 m above the surface topography and spaced 10 m apart.

# Define the observation locations as an (N, 3) numpy array or load them from a file.
x = np.linspace(-80.0, 80.0, 17)
y = np.linspace(-80.0, 80.0, 17)
x, y = np.meshgrid(x, y)
x, y = mkvc(x.T), mkvc(y.T)
fun_interp = LinearNDInterpolator(np.c_[x_topo, y_topo], z_topo)
z = fun_interp(np.c_[x, y]) + 5.0
receiver_locations = np.c_[x, y, z]

# Define the component(s) of the field we want to simulate as strings within
# a list. Here we measure the x, y and z derivatives of the vertical gravity
# anomaly at each observation location.
components = ["gxz", "gyz", "gzz"]

# Use the observation locations and components to define receivers for the entire survey
# in one step. The set of receivers, even if it's only 1, are organized within a list.
receiver_list = gravity.receivers.Point(receiver_locations, components=components)
receiver_list = [receiver_list]

# Defining the source. For gravity surveys, we simply need to specific the list of
# receivers associated with the source field.
source_field = gravity.sources.SourceField(receiver_list=receiver_list)

# Defining the survey.
survey = gravity.survey.Survey(source_field)

If desired, we can extract various objects and properties from the objects used to generate the survey. E.g.

print("# of locations: {}".format(survey.nRx))  # number of receiver locations
print("# of data: {}".format(survey.nD))  # number of data that will be simulated
print(survey.source_field)  # the source field object
print(survey.source_field.receiver_list[0])  # the receiver object
print(receiver_list[0].locations[:5, :])  # the first 5 receiver locations

# of locations: 289
# of data: 867
<simpeg.potential_fields.gravity.sources.SourceField object at 0x7ff881365f60>
<simpeg.potential_fields.gravity.receivers.Point object at 0x7ff88123d810>
[[-80.         -80.         103.45749978]
 [-70.         -80.         102.92439828]
 [-60.         -80.         102.04004226]
 [-50.         -80.         101.42653248]
 [-40.         -80.         100.7063376 ]]

Design a (Tree) Mesh¶

Meshes are designed using the discretize package. See the discretize user tutorials to learn more about creating meshes. Here, the forward simulation is computed for a tree mesh. If you wanted to generate a tensor mesh instead, you can use the code snippet from the 3D Forward Simulation of Gravity Anomaly Data tutorial.

The integral formulation for gravity essentially sums the independent contribution for every voxel cell in the mesh. Since the kernel function that computes the contribution for a single cell is an analytic solution, small cells are not required to accurately compute the contributions from coarse structures with constant density (e.g. a rectangular prism). For complex structures however, or to define surface topography more accurately, finer cells may be needed. Furthermore, cells do not need to be cubic.

Here, a minimum cell width of 5 m is used within our survey region. In this tutorial, we discretize finely along the surface topography, and within our region of interest. However, a multitude of refinement methods can be applied when generating tree meshes.

dx = 5  # minimum cell width (base mesh cell width) in x
dy = 5  # minimum cell width (base mesh cell width) in y
dz = 5  # minimum cell width (base mesh cell width) in z

x_length = 240.0  # domain width in x
y_length = 240.0  # domain width in y
z_length = 120.0  # domain width in z

# Compute number of base mesh cells required in x and y
nbcx = 2 ** int(np.round(np.log(x_length / dx) / np.log(2.0)))
nbcy = 2 ** int(np.round(np.log(y_length / dy) / np.log(2.0)))
nbcz = 2 ** int(np.round(np.log(z_length / dz) / np.log(2.0)))

# Define the base mesh. Top defined at z = 0 m.
hx = [(dx, nbcx)]
hy = [(dy, nbcy)]
hz = [(dz, nbcz)]
mesh = TreeMesh([hx, hy, hz], x0="CCN", diagonal_balance=True)

# Shift vertically to top same as maximum topography
mesh.origin += np.r_[0.0, 0.0, z_topo.max()]

# Refine based on surface topography
mesh.refine_surface(topo_xyz, padding_cells_by_level=[2, 2], finalize=False)

# Refine box based on region of interest
wsb_corner = np.c_[-100, -100, 20]
ent_corner = np.c_[100, 100, 100]
# Note -1 is a flag for smallest cell size
mesh.refine_box(wsb_corner, ent_corner, levels=[-1], finalize=False)

mesh.finalize()

If desired, we can extract various properties of the mesh. E.g.

print("# of cells: {}".format(mesh.n_cells))  # Number of cells
print("# of x-faces: {}".format(mesh.n_faces_x))  # Number of x-faces
print("Origin: {}".format(mesh.origin))  # bottom-southewest corner
print("Max cell volume: {}".format(mesh.cell_volumes.max()))  # Largest cell size
print(mesh.cell_centers[0:5, :])  # Cell center locations

# of cells: 46260
# of x-faces: 46082
Origin: [-160.         -160.          -59.50266358]
Max cell volume: 64000.0
[[-140.         -140.          -39.50266358]
 [-100.         -140.          -39.50266358]
 [-140.         -100.          -39.50266358]
 [-100.         -100.          -39.50266358]
 [-150.         -150.           -9.50266358]]

Define the Active Cells¶

Whereas cells below the Earth’s surface contribute towards the simulated gravity anomaly, air cells do not. The set of mesh cells used in the forward simulation are referred to as ‘active cells’. Unused cells (air cells) are ‘inactive cells’. Here, the discretize active_from_xyz utility function is used to find the indices of the active cells using the mesh and surface topography. The output quantity is a bool array.

# Indices of the active mesh cells from topography (e.g. cells below surface)
active_cells = active_from_xyz(mesh, topo_xyz)

Mapping from the Model to Active Cells¶

In SimPEG, the term ‘model’ is not synonymous with the physical property values defined on the mesh. For example, the model may be defined as the logarithms of the physical property values, or be parameters defining a layered Earth. When simulating gravity anomaly data using the integral formulation, we must define a mapping from the set of model parameters to the active cells in the mesh. Mappings are created using the simpeg.maps module. For the tutorial exercise, the model is the density contrast values for all active cells. As such, our mapping is an identity mapping, whose dimensions are equal to the number of active cells.

# Define mapping from model to active cells. The model consists of a density
# contrast value for each cell below the Earth's surface.
n_active = int(active_cells.sum())
model_map = maps.IdentityMap(nP=n_active)

Define the Model¶

Here, we create the model that will be used to predict gravity anomaly data. Recall that our model is the density constrast values for all active mesh cells. So the model is a 1D numpy.ndarray whose length is equal to the number of model parameters. In SimPEG, density contrast values are defined in units of g/cc. Here, the model consists of a less dense block and a more dense sphere. We plot the model using the plot_slice method.

# Define density contrast values for each unit in g/cc
background_density = 0.0
block_density = -0.2
sphere_density = 0.2

# Instantiate a vector array. Models in SimPEG are vector arrays.
model = background_density * np.ones(n_active)

# You could find the indicies of specific cells within the model and change their
# values to add structures.
ind_block = (
    (mesh.cell_centers[active_cells, 0] > -50.0)
    & (mesh.cell_centers[active_cells, 0] < -20.0)
    & (mesh.cell_centers[active_cells, 1] > -15.0)
    & (mesh.cell_centers[active_cells, 1] < 15.0)
    & (mesh.cell_centers[active_cells, 2] > 50.0)
    & (mesh.cell_centers[active_cells, 2] < 70.0)
)
model[ind_block] = block_density

# You can also use SimPEG utilities to add structures to the model more concisely
ind_sphere = model_builder.get_indices_sphere(
    np.r_[35.0, 0.0, 60.0], 14.0, mesh.cell_centers
)
ind_sphere = ind_sphere[active_cells]
model[ind_sphere] = sphere_density

# Map for ignoring inactive cells when plotting
plotting_map = maps.InjectActiveCells(mesh, active_cells, np.nan)

# Plot Density Contrast Model
fig = plt.figure(figsize=(8, 3.5))
ax1 = fig.add_axes([0.1, 0.12, 0.73, 0.78])

norm = mpl.colors.Normalize(vmin=np.min(model), vmax=np.max(model))

mesh.plot_slice(
    plotting_map * model,
    normal="Y",
    ax=ax1,
    ind=int(mesh.shape_cells[1] / 2),
    grid=True,
    pcolor_opts={"cmap": mpl.cm.RdYlBu_r, "norm": norm},
)
ax1.set_title("Model slice at y = 0 m")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("z (m)")

ax2 = fig.add_axes([0.85, 0.12, 0.03, 0.78])

cbar = mpl.colorbar.ColorbarBase(
    ax2, norm=norm, orientation="vertical", cmap=mpl.cm.RdYlBu_r
)
cbar.set_label("$g/cm^3$", rotation=270, labelpad=15, size=16)

plt.show()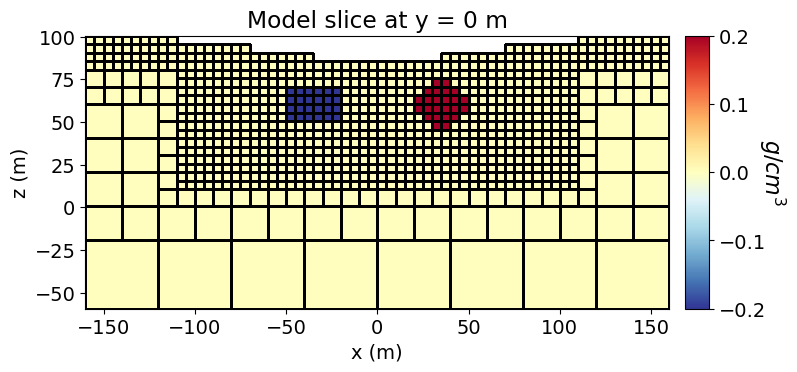

/t40array/ssoler/miniforge3/envs/simpeg-user-tutorials/lib/python3.10/site-packages/discretize/mixins/mpl_mod.py:2152: FutureWarning: In discretize v1.0 the TreeMesh will change the default value of diagonal_balance to True, which will likely slightly change meshes you havepreviously created. If you need to keep the current behavoir, explicitly set diagonal_balance=False.
  temp_mesh = discretize.TreeMesh(h2d, x2d)

Define the Forward Simulation¶

In SimPEG, the physics of the forward simulation is defined by creating an instance of an appropriate simulation class. In this case, the simulation class corresponds to a 3D integral formulation. To fully define the forward simulation, we need to connect the simulation object to:

the survey
the mesh
the indices of the active cells
the mapping from the model to the active cells

This is accomplished by setting each one of the aforementioned items as a property of the simulation object. Additional keyword arguments can also be set which impact the forward simulation. Because we are only simulating data for a single model, there is no benefit to storing the sensitivities for the forward simulation. As a result, we set the store_sensitivities property to “forward_only”.

simulation = gravity.simulation.Simulation3DIntegral(
    survey=survey,
    mesh=mesh,
    rhoMap=model_map,
    active_cells=active_cells,
    store_sensitivities="forward_only",
    engine="choclo",
)

Simulate Gravity Gradiometry Data¶

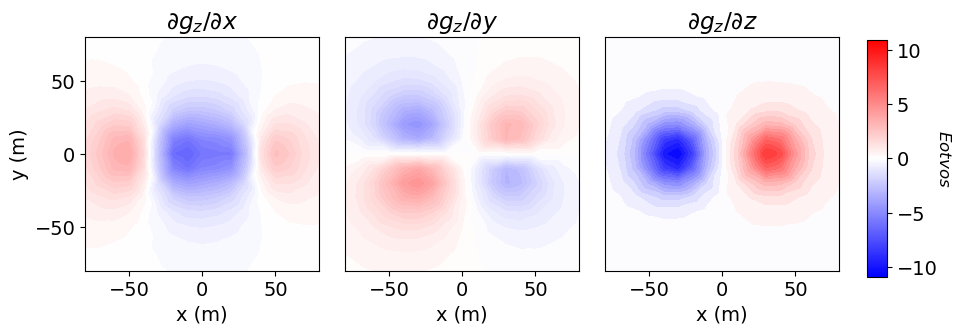
Once any simulation within SimPEG has been properly constructed, simulated data for a given model vector can be computed using the dpred method. SimPEG uses a right-handed coordinate system to simulate gravity gradiometry data where Z is positive upward!!! Please be aware of this when using gravity gradiometry data to infer the locations of more and less dense structures. In SimPEG, gravity gradiometry values are in units Eotvos, where 1 E = $10^{-9} \; s^{-2}$ = 10^-4 mGal/m.

dpred = simulation.dpred(model)

Data are ordered by component, then by location. Here, we reshape the predicted data vector into an array for easier plotting.

n_loc = survey.nRx  # Number of receiver locations
n_comp = len(components)  # Number of data components
dpred_plotting = np.reshape(dpred, (n_loc, n_comp))

# Plot
fig = plt.figure(figsize=(10, 3))
v_max = np.max(np.abs(dpred))

ax = 3 * [None]
cplot = 3 * [None]
comp_list = ["x", "y", "z"]

norm = mpl.colors.Normalize(vmin=-v_max, vmax=v_max)

for ii in range(0, 3):
    ax[ii] = fig.add_axes([0.1 + ii * 0.26, 0.15, 0.25, 0.78])
    cplot[ii] = plot2Ddata(
        receiver_locations,
        dpred_plotting[:, ii],
        ax=ax[ii],
        ncontour=30,
        contourOpts={"cmap": "bwr", "norm": norm},
    )
    ax[ii].set_title(r"$\partial g_z /\partial {}$".format(comp_list[ii]))
    ax[ii].set_xlabel("x (m)")
    if ii == 0:
        ax[ii].set_ylabel("y (m)")
    else:
        ax[ii].set_yticks([])

cx = fig.add_axes([0.89, 0.13, 0.02, 0.79])
cbar = mpl.colorbar.ColorbarBase(cx, norm=norm, orientation="vertical", cmap=mpl.cm.bwr)
cbar.set_label("$Eotvos$", rotation=270, labelpad=10, size=12)

plt.show()

SimPEG User Tutorials

3D Forward Simulation of Gravity Anomaly Data

SimPEG User Tutorials

3D Inversion of Gravity Anomaly Data