Keywords: DC resistivity, 2.5D inversion, sparse norm, tree mesh.
Summary: Here we invert DC resistivity data on a tree mesh to recover the subsurface distribution of electric properties. To demonstrate a range of functionality within SimPEG, we apply two approaches:
Weighted least-squares inversion, where we invert normalized voltage data to recover a log-conductivity model
Iteratively re-weighted least-squares (IRLS) inversion, where we invert apparent resistivity data to recover a log-resistivity model
The weighted least-squares approach is a great introduction to geophysical inversion with SimPEG. One drawback however, is that it recovers smooth structures which may not be representative of the true model. The iteratively re-weighted least-squares approach is able to recover sparse and/or blocky structures. Because this tutorial focusses primarily on inversion-related functionality, we urge the reader to become familiar with functionality explained in the 2.5D Forward Simulation tutorial before working through this one.
Learning Objectives:
Introduce geophysical inversion with SimPEG.
Assigning appropriate uncertainties to normalized voltage and apparent resistivity data.
Designing a suitable mesh for 2.5D DC resistivity inversion.
Choosing suitable parameters for the inversion.
Specifying directives that are applied throughout the inversion.
Apply the sensitivity weighting commonly used when inverting magnetic data.
Inversion with weighted least-squares and sparse-norm regularizations.
Analyzing inversion outputs.
Import Modules¶
Here, we import all of the functionality required to run the notebook for the tutorial exercise.
All of the functionality specific to DC resistivity is imported from simpeg
# SimPEG functionality
from simpeg.electromagnetics.static import resistivity as dc
from simpeg.electromagnetics.static.utils.static_utils import (
plot_pseudosection,
generate_survey_from_abmn_locations,
apparent_resistivity_from_voltage,
)
from simpeg.utils.io_utils.io_utils_electromagnetics import read_dcip2d_ubc
from simpeg.utils import download, model_builder
from simpeg import (
maps,
data,
data_misfit,
regularization,
optimization,
inverse_problem,
inversion,
directives,
)
# discretize functionality
from discretize import TreeMesh
from discretize.utils import active_from_xyz
# Basic Python functionality
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import tarfile
mpl.rcParams.update({"font.size": 14}) # default font size
cmap = mpl.cm.RdYlBu_r # default colormapLoad Tutorial Data and Plot¶
For most geophysical inversion projects, a reasonable inversion result can be obtained so long as the practitioner has observed data, the survey geometry and topography. For this tutorial, the observed data and topography files are provided. Here, we download and import the observed data and topography into the SimPEG framework.
# URL to download from repository assets
data_source = "https://github.com/simpeg/user-tutorials/raw/main/assets/05-dcr/inv_dcr_2d_files.tar.gz"
# download the data
downloaded_data = download(data_source, overwrite=True)
# unzip the tarfile
tar = tarfile.open(downloaded_data, "r")
tar.extractall()
tar.close()
# path to the directory containing our data
dir_path = downloaded_data.split(".")[0] + os.path.sep
# files to work with
topo_filename = dir_path + "topo_2d.txt"
data_filename = dir_path + "dc_data.obs"overwriting /home/ssoler/git/user-tutorials/notebooks/05-dcr/inv_dcr_2d_files.tar.gz
Downloading https://github.com/simpeg/user-tutorials/raw/main/assets/05-dcr/inv_dcr_2d_files.tar.gz
saved to: /home/ssoler/git/user-tutorials/notebooks/05-dcr/inv_dcr_2d_files.tar.gz
Download completed!
/tmp/ipykernel_843793/4068670249.py:9: DeprecationWarning: Python 3.14 will, by default, filter extracted tar archives and reject files or modify their metadata. Use the filter argument to control this behavior.
tar.extractall()
Load the Topography¶
True surface topography is defined as an (N, 3) numpy.ndarray. For the 2.5D problem geometry however, topography is an (N, 2) numpy.ndarray, where the first coordinate represent along-line position and the second coordinate represents the vertical position. In this tutorial, we assume the topography and electrode locations are defined according to the 2.5D geometry.
# Load 2D topography
topo_2d = np.loadtxt(str(topo_filename))# Plot 2D topography
fig = plt.figure(figsize=(10, 2))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8])
ax.plot(topo_2d[:, 0], topo_2d[:, -1], color="b", linewidth=1)
ax.set_xlim([topo_2d[:, 0].min(), topo_2d[:, 0].max()])
ax.set_xlabel("x (m)", labelpad=5)
ax.set_ylabel("z (m)", labelpad=5)
ax.grid(True)
ax.set_title("Topography (Exaggerated z-axis)", fontsize=16, pad=10)
plt.show(fig)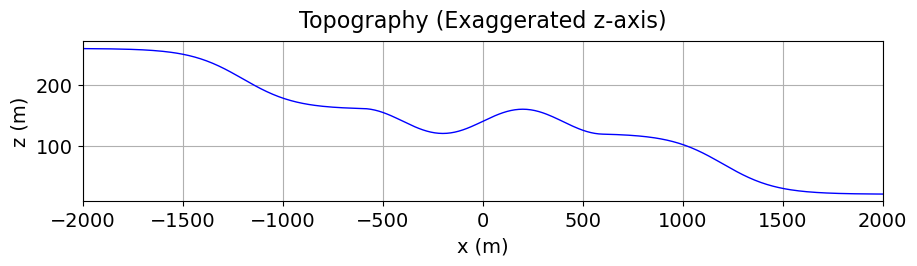
Load DC Resistivity Data¶
Option A: DCIP2D formatted data
For this tutorial, the observed data are organized with a UBC-GIF DCIP2D formatted data file. We can use the read_dcip2d_ubc utility function to load data in this format. This function outputs a SimPEG Data object. The data are normalized voltages in units V/A.
voltage_data = read_dcip2d_ubc(data_filename, "volt", "general")Option B: Survey from ABMN electrode locations
If you have CSV-formatted data containing the ABMN electrode locations, you will need to:
load the file into a numpy.ndarray
extract the data column and the A, B, M and N electrode locations
transform the electrode locations to the 2.5D geometry if necessary; i.e. (N, 2) numpy.ndarray
use the generate
_survey _from _abmn _locations to generate a survey object automatically. Define a Data object attached to the survey and observed data.
E.g. for a file containing electrode locations already formatted for a 2.5D geometry:
data_array = np.loadtxt(data_filename, skiprows=1)
dobs = data_array[:, -1]
A = data_array[:, 0:2]
B = data_array[:, 2:4]
M = data_array[:, 4:6]
N = data_array[:, 6:8]
survey = generate_survey_from_abmn_locations(
locations_a=A,
locations_b=B,
locations_m=M,
locations_n=M,
data_type='volt'
)
dc_data = data.Data(survey, dobs=dobs)Plot DC Resistivity Data in Pseudo-Section¶
Here we use the plot_pseudosection utility function to plot the normalized voltage data in pseudosection. We also use the apparent
# Plot voltages pseudo-section
fig = plt.figure(figsize=(8, 2.75))
ax1 = fig.add_axes([0.1, 0.15, 0.75, 0.78])
plot_pseudosection(
voltage_data,
plot_type="scatter",
ax=ax1,
scale="log",
cbar_label="V/A",
scatter_opts={"cmap": mpl.cm.viridis},
)
ax1.set_title("Normalized Voltages")
plt.show()
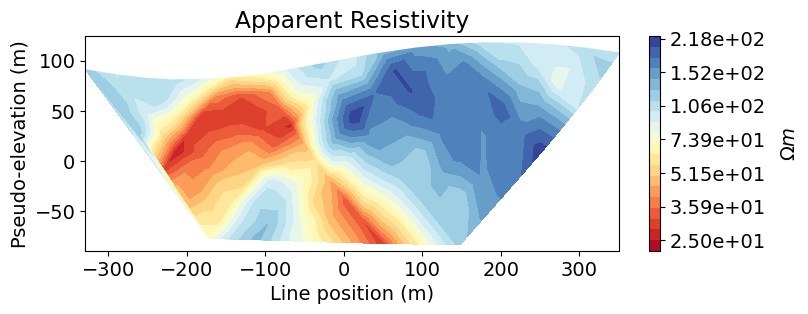
# Get apparent conductivities from volts and survey geometry
apparent_resistivities = apparent_resistivity_from_voltage(
voltage_data.survey, voltage_data.dobs
)
# Plot apparent resistivity pseudo-section
fig = plt.figure(figsize=(8, 2.75))
ax1 = fig.add_axes([0.1, 0.15, 0.75, 0.78])
plot_pseudosection(
voltage_data.survey,
apparent_resistivities,
plot_type="contourf",
ax=ax1,
scale="log",
cbar_label=r"$\Omega m$",
mask_topography=True,
contourf_opts={"levels": 20, "cmap": mpl.cm.RdYlBu},
)
ax1.set_title("Apparent Resistivity")
plt.show()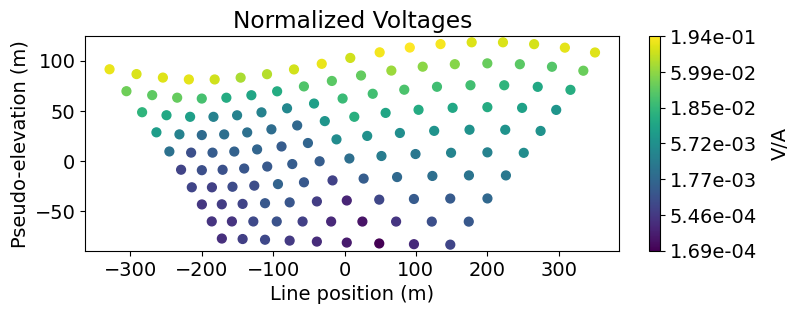
Assign Uncertainties¶
Inversion with SimPEG requires that we define the uncertainties on our data; that is, an estimate of the standard deviation of the noise on our data assuming it is uncorrelated Gaussian with zero mean. An online resource explaining uncertainties and their role in the inversion can be found here.
For normalized voltage data, we generally apply a percent uncertainty and a very small floor uncertainty to all data. Differences in electrode spacing and subsurface conductivity result in measured voltages that span many orders of magnitude. A percent uncertainty ensures all data are fit equally. Depending on the quality of the data, we may choose a percent uncertainty between 2% - 10%. The floor uncertainty ensures stability when there are zero-crossings or erroneously small voltages. Here, we apply uncertainties of 1e-7 V/A + 5 %.
For apparent resistivity data, we also apply a percent uncertainty and a very small floor uncertainty to all data. A percent uncertainty will fit conductive and resistive structures equally; unlike a floor uncertainty which will prioritize fitting more resistive structures. Depending on the quality of the data, we may choose a percent uncertainty between 2% - 10%. The floor uncertainty ensures stability when there are zero-crossings or erroneously small voltages.
# Apply uncertainties to normalized voltage data
voltage_data.standard_deviation = 1e-7 + 0.05 * np.abs(voltage_data.dobs)Design a (Tree) Mesh¶
The same rules for defining appropriate meshes for forward simulation of DC resistivity apply to inversion. Please visit the 2.5D Forward Simulation tutorial to see the best practices for mesh design.
Tutorial mesh: Here, a minimum cell width of 4 m (or 1/10 the minimum electrode spacing) is used within our survey region. The largest electrode spacing was 400 m, so a the padding was extended at least 1200 m from the survey region. Using the refine_surface method, we refine the tree mesh where there is significant topography. And using the refine_points methods, we refine based on electrodes locations. Visit the tree mesh API to see additional refinement methods.
dh = 4 # base cell width
dom_width_x = 3200.0 # domain width x
dom_width_z = 2400.0 # domain width z
nbcx = 2 ** int(np.round(np.log(dom_width_x / dh) / np.log(2.0))) # num. base cells x
nbcz = 2 ** int(np.round(np.log(dom_width_z / dh) / np.log(2.0))) # num. base cells z
# Define the base mesh with top at z = 0 m
hx = [(dh, nbcx)]
hz = [(dh, nbcz)]
mesh = TreeMesh([hx, hz], x0="CN", diagonal_balance=True)
# Shift top to maximum topography
mesh.origin = mesh.origin + np.r_[0.0, topo_2d[:, -1].max()]
# Mesh refinement based on topography
mesh.refine_surface(
topo_2d,
padding_cells_by_level=[0, 0, 4, 4],
finalize=False,
)
# Extract unique electrode locations.
unique_locations = voltage_data.survey.unique_electrode_locations
# Mesh refinement near electrodes.
mesh.refine_points(
unique_locations, padding_cells_by_level=[8, 12, 6, 6], finalize=False
)
mesh.finalize()Define the Active Cells¶
Simulated geophysical data are dependent on the subsurface distribution of physical property values. As a result, the cells lying below the surface topography are commonly referred to as ‘active cells’. And air cells, whose physical property values are fixed, are commonly referred to as ‘inactive cells’. Here, the discretize active_from_xyz utility function is used to find the indices of the active cells using the mesh and surface topography. The output quantity is a bool array.
# Indices of the active mesh cells from topography (e.g. cells below surface)
active_cells = active_from_xyz(mesh, topo_2d)
# number of active cells
n_active = np.sum(active_cells)Project Electrodes to Discretized Topography¶
Surface DC resistivity data will not be modeled accurately if the electrodes are modeled as living above or below the surface. It is especially problematic when electrodes are modeled as living in the air. Prior to inverting DC resistivity data, we must project the electrodes from their true elevation to the surface of the discretized topography. This is done using the drape
voltage_data.survey.drape_electrodes_on_topography(
mesh, active_cells, topo_cell_cutoff="top"
)Weighted Least-Squares Inversion¶
Here, a weighted least-squares inversion approach is used to invert normalized voltage data to recover a log-conductivity model. We invert for log-conductivity because
It naturally enforces positive conductivity values in the recovered model
Electrical conductivity is a physical property that spans many orders of magnitude
Mapping from the Model to the Mesh¶
In SimPEG, the term ‘model’ is not synonymous with the physical property values defined on the mesh. For whatever model we choose, we must define a mapping from the set of model parameters (a 1D numpy.ndarray) to the physical property values of all cells in the mesh. Mappings are created using the simpeg.maps module.
For DC resistivity, the model parameters define the subsurface electrical conductivity, and the electrical conductivities of the cells in the air are given a fixed value. Here, the model defines the log-conductivity values for all active cells. We use the simpeg.maps.ExpMap to map from the model parameters to the conductivity values for all active cells. Then we use the simpeg
# Map model parameters to all cells
log_conductivity_map = maps.InjectActiveCells(mesh, active_cells, 1e-8) * maps.ExpMap(
nP=n_active
)Starting/Reference Models¶
The starting model defines a reasonable starting point for the inversion and does not necessarily represent an initial estimate of the true model. It should be noted that the starting model cannot be vector of zeros, otherwise the inversion will be unable to compute a gradient direction at the first iteration. For DC resistivity inversion, the starting model is frequently a halfspace estimated from the set of apparent resistivities/conductivities.
The reference model is used to include a-priori information. By default, the starting model is set as the reference model. The impact of the reference model on the inversion will be discussed in another tutorial.
Notice that the length of the starting and reference models is equal to the number of model parameters!!!
# Median apparent resistivity
median_resistivity = np.median(apparent_resistivities)
# Create starting model from log-conductivity
starting_conductivity_model = np.log(1 / median_resistivity) * np.ones(n_active)
# Zero reference conductivity model
reference_conductivity_model = starting_conductivity_model.copy()Define the Forward Simulation¶
A simulation object defining the forward problem is required in order to predict data and calculate misfits for recovered models. A comprehensive description of the simulation object for 2.5D DC resistivity was discussed in the 2.5D Forward Simulation tutorial. Here, we use the Simulation2DNodal simulation which solves for the electric potential on mesh nodes.
Since our model consists of log-conductivities, we use sigmaMap to set the mapping from the model to the mesh cells. Except for in extreme cases, we can compute and store the Jacobian explicitly for 2.5D problems. By doing so, we drastically reduce the run-time of the inversion.
voltage_simulation = dc.simulation_2d.Simulation2DNodal(
mesh, survey=voltage_data.survey, sigmaMap=log_conductivity_map, storeJ=True
)INFO: Setting the default solver 'Pardiso' for the 'Simulation2DNodal'.
To avoid receiving this message, pass a solver to the simulation. For example:
from simpeg.utils import get_default_solver
solver = get_default_solver()
simulation = Simulation2DNodal(solver=solver, ...)
Define the Data Misfit¶
To understand the role of the data misfit in the inversion, please visit this online resource. Here, we use the L2DataMisfit class to define the data misfit. In this case, the data misfit is the L2 norm of the weighted residual between the observed data and the data predicted for a given model. When instantiating the data misfit object within SimPEG, we must assign an appropriate data object and simulation object as properties.
dmis_L2 = data_misfit.L2DataMisfit(simulation=voltage_simulation, data=voltage_data)Define the Regularization¶
To understand the role of the regularization in the inversion, please visit this online resource. Here, we use the WeightedLeastSquares regularization class to constrain the inversion result. Here, the scaling constants that balance the smallness and smoothness terms are set directly. We use the inverse square of the smallest cell size to balance the smallness and smoothness terms. Setting alpha_s to a very small value will recover the smoothest model. And the reference model is only applied to the smallness term.
By default, the regularization acts on the model parameters; which in the case are the log-conductivities of the active cells. So we need to specify which cells are active in the regularization. And if we wanted to apply the regularization to a function of the model parameters, we would need to set an approprate mapping object using the mapping keyword argument.
reg_L2 = regularization.WeightedLeastSquares(
mesh,
active_cells=active_cells,
alpha_s=dh**-2,
alpha_x=1,
alpha_y=1,
reference_model=reference_conductivity_model,
reference_model_in_smooth=False,
)Define the Optimization Algorithm¶
Here, we use the InexactGaussNewton class to solve the optimization problem using the inexact Gauss Newton with conjugate gradient solver. Reasonable default values have generally been set for the properties of each optimization class. However, the user may choose to set custom values; e.g. the accuracy tolerance for the conjugate gradient solver or the number of line searches.
opt_L2 = optimization.InexactGaussNewton(
maxIter=40, maxIterLS=20, cg_maxiter=20, cg_rtol=1e-3
)Define the Inverse Problem¶
We use the BaseInvProblem class to fully define the inverse problem that is solved at each beta (trade-off parameter) iteration. The inverse problem requires appropriate data misfit, regularization and optimization objects.
inv_prob_L2 = inverse_problem.BaseInvProblem(dmis_L2, reg_L2, opt_L2)Provide Inversion Directives¶
Directives represent operations that are carried out during the inversion. Here, we apply common directives for weighted least-squares inversion of DC resistivity data and describe their roles. These are:
UpdateSensitivityWeights: Apply sensitivity weighting to counteract the natural tendency of DC resistivity inversion to place materials near the electrodes. Since the problem is non-linear and the sensitivities are updated with every model, we set
every_iteration=True. For DC resistivity inversion, we do not want to use the entire dynamic range of the sensitivities to generate our weighting. So we generally setthreshold_valueto a value betwewen 1e-5 and 1e-3.UpdatePreconditioner: Apply Jacobi preconditioner when solving optimization problem to reduce the number of conjugate gradient iterations. We set
update_every_iteration=Truebecause the ideal preconditioner is model-dependent.BetaEstimate_ByEig: Compute and set starting trade-off parameter (beta) based on largest eigenvalues.
BetaSchedule: Size reduction of the trade-off parameter at every beta iteration, and the number of Gauss-Newton iterations for each beta. In general, a
coolingFactorbetween 1.5 and 2.5, andcoolingRateof 2 or 3 works well for DC resistivity inversion. Cooling beta too quickly will result in portions of the model getting trapped in local minima. And we will not be finding the solution that minimizes the optimization problem if the cooling rate is too small.TargetMisfit: Terminates the inversion when the data misfit equals the target misfit. A
chifact=1terminates the inversion when the data misfit equals the number of data.
The directive objects are organized in a list. Upon starting the inversion or updating the recovered model at each iteration, the inversion will call each directive within the list in order. The order of the directives matters, and SimPEG will throw an error if directives are organized into an improper order. Some directives, like the BetaEstimate_ByEig are only used when starting the inversion. Other directives, like UpdatePreconditionner, are used whenever the model is updated.
sensitivity_weights = directives.UpdateSensitivityWeights(
every_iteration=True, threshold_value=1e-2
)
update_jacobi = directives.UpdatePreconditioner(update_every_iteration=True)
starting_beta = directives.BetaEstimate_ByEig(beta0_ratio=10)
beta_schedule = directives.BetaSchedule(coolingFactor=2.0, coolingRate=2)
target_misfit = directives.TargetMisfit(chifact=1.0)
directives_list_L2 = [
sensitivity_weights,
update_jacobi,
starting_beta,
beta_schedule,
target_misfit,
]Define and Run the Inversion¶
We define the inversion using the BaseInversion class. The inversion class must be instantiated with an appropriate inverse problem object and directives list. The run method, along with a starting model, is respondible for running the inversion. The output is a 1D numpy.ndarray containing the recovered model parameters
# Here we combine the inverse problem and the set of directives
inv_L2 = inversion.BaseInversion(inv_prob_L2, directives_list_L2)
# Run the inversion
# recovered_model_L2 = inv_L2.run(np.log(0.01) * np.ones(n_param))
recovered_log_conductivity_model = inv_L2.run(starting_conductivity_model)
Running inversion with SimPEG v0.25.0
INFO: Directive TargetMisfit: Target data misfit is 135.0
============================ Inexact Gauss Newton ============================
# beta phi_d phi_m f |proj(x-g)-x| LS Comment
-----------------------------------------------------------------------------
0 2.42e+01 4.42e+04 0.00e+00 4.42e+04
1 2.42e+01 1.71e+03 5.00e+01 2.92e+03 5.31e+03 0
2 2.42e+01 4.23e+02 7.69e+01 2.28e+03 4.29e+02 0
3 1.21e+01 2.22e+02 9.10e+01 1.32e+03 7.60e+01 0
4 1.21e+01 2.25e+02 8.95e+01 1.31e+03 7.29e+00 0
5 6.05e+00 1.37e+02 1.00e+02 7.44e+02 4.38e+01 0
6 6.05e+00 1.38e+02 9.81e+01 7.32e+02 3.91e+00 0
7 3.02e+00 1.02e+02 1.07e+02 4.26e+02 2.31e+01 0
------------------------- STOP! -------------------------
1 : |fc-fOld| = 1.0893e+01 <= tolF*(1+|f0|) = 4.4222e+03
1 : |xc-x_last| = 2.6596e+00 <= tolX*(1+|x0|) = 3.8989e+01
0 : |proj(x-g)-x| = 2.3053e+01 <= tolG = 1.0000e-01
0 : |proj(x-g)-x| = 2.3053e+01 <= 1e3*eps = 1.0000e-02
0 : maxIter = 40 <= iter = 7
------------------------- DONE! -------------------------
Plot the Data Misfit¶
This step is necessary for determining whether the recovered model accurately reproduces observed anomalies. Here, we plot the observed data, predicted data for the recovered model, and the normalized data misfit. As we can see, the recovered model reproduces the observed data quite well. And the normalized misfit map indicates we are not overfitting certain electrodes relative to others.
If desired, one could also use the apparent
# Predicted data from recovered model
dpred = inv_prob_L2.dpred
dobs = voltage_data.dobs
std = voltage_data.standard_deviation
# Plot
fig = plt.figure(figsize=(9, 11))
data_array = [np.abs(dobs), np.abs(dpred), (dobs - dpred) / std]
plot_title = ["Observed Voltage", "Predicted Voltage", "Normalized Misfit"]
plot_units = ["V/A", "V/A", ""]
scale = ["log", "log", "linear"]
cmap_list = [mpl.cm.viridis, mpl.cm.viridis, mpl.cm.RdYlBu]
ax1 = 3 * [None]
cax1 = 3 * [None]
cbar = 3 * [None]
cplot = 3 * [None]
for ii in range(0, 3):
ax1[ii] = fig.add_axes([0.15, 0.72 - 0.33 * ii, 0.65, 0.21])
cax1[ii] = fig.add_axes([0.81, 0.72 - 0.33 * ii, 0.03, 0.21])
cplot[ii] = plot_pseudosection(
voltage_data.survey,
data_array[ii],
"contourf",
ax=ax1[ii],
cax=cax1[ii],
scale=scale[ii],
cbar_label=plot_units[ii],
mask_topography=True,
contourf_opts={"levels": 25, "cmap": cmap_list[ii]},
)
ax1[ii].set_title(plot_title[ii])
plt.show()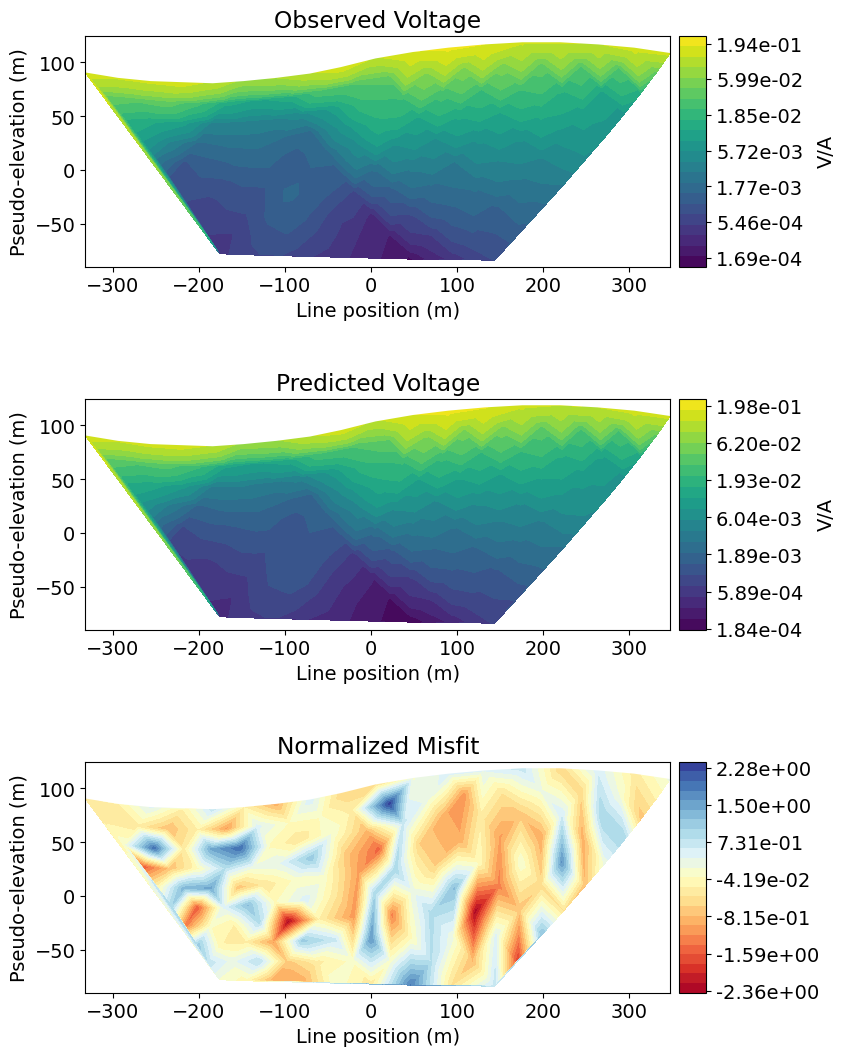
Plot the Recovered Model¶
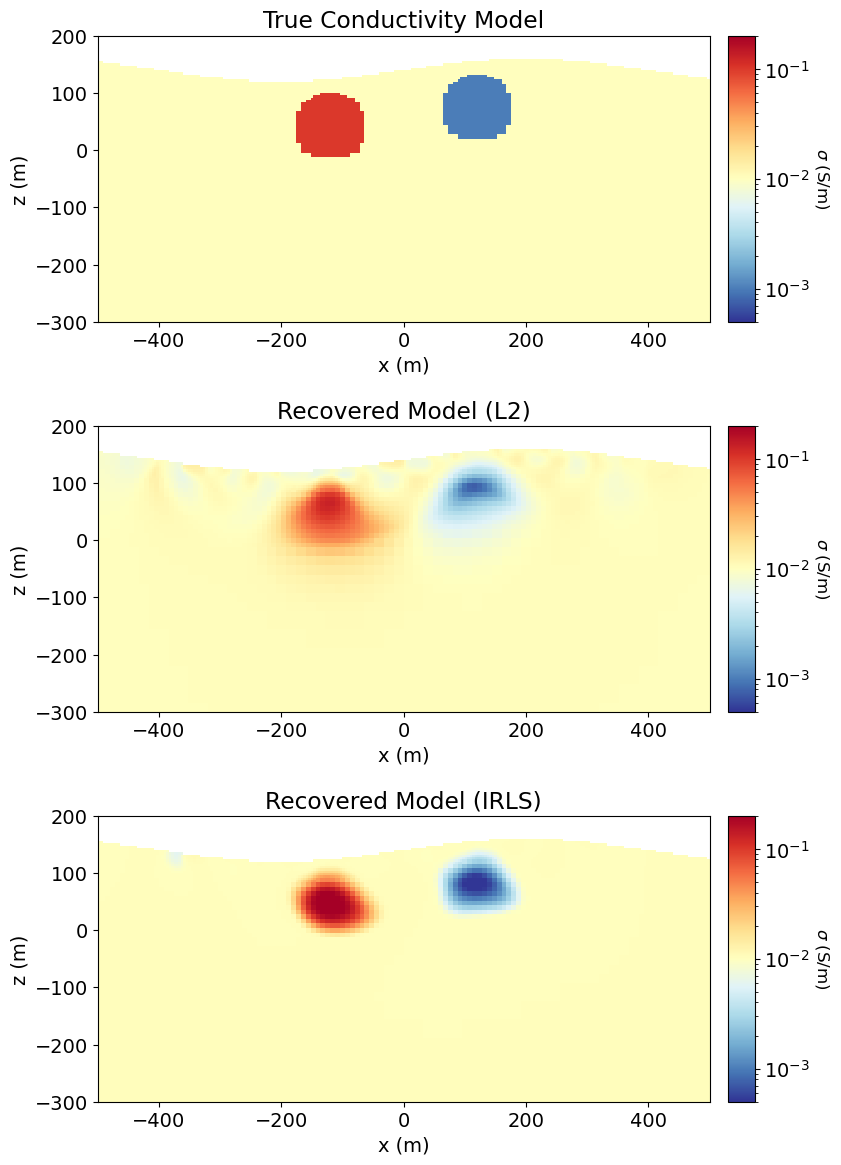
As we can see, weighted least-squares regularization leads to the recovery of smooth models.
# Convert log-conductivity values to conductivity values
recovered_conductivity_L2 = np.exp(recovered_log_conductivity_model)# Define a mapping to plot models and ignore inactive cells
plotting_map = maps.InjectActiveCells(mesh, active_cells, np.nan)norm = LogNorm(vmin=5e-4, vmax=2e-1)
fig = plt.figure(figsize=(9, 4))
ax1 = fig.add_axes([0.14, 0.17, 0.68, 0.7])
mesh.plot_image(
plotting_map * recovered_conductivity_L2,
normal="Y",
ax=ax1,
grid=False,
pcolor_opts={"norm": norm, "cmap": mpl.cm.RdYlBu_r},
)
ax1.set_xlim(-500, 500)
ax1.set_ylim(-300, 200)
ax1.set_title("Recovered Conductivity Model (L2)")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("z (m)")
ax2 = fig.add_axes([0.84, 0.17, 0.03, 0.7])
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", cmap=mpl.cm.RdYlBu_r
)
cbar.set_label(r"$\sigma$ (S/m)", rotation=270, labelpad=15, size=12)
plt.show()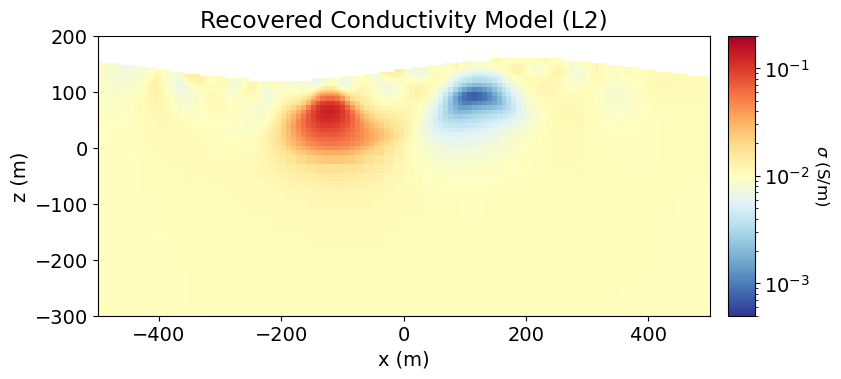
Iteratively Re-weighted Least-Squares Inversion¶
Here, we provide a step-by-step best-practices approach for IRLS inversion of apparent resistivity data on a tree mesh to recover a log-resistivity model. Many of the steps are the same as our previous approach. As a result, we will avoid repeating information whenever possible.
Define An Apparent Resistivity Survey¶
We cannot reuse a survey that was used to simulate a different data type. So we must define a new survey object for inverting apparent resistivity data. This can be done by extracting the ABMN electrode locations from the previous survey object and using the generate
# Extract ABMN electrode locations from previous survey object
locations_a = voltage_data.survey.locations_a.copy()
locations_b = voltage_data.survey.locations_b.copy()
locations_m = voltage_data.survey.locations_m.copy()
locations_n = voltage_data.survey.locations_n.copy()
# Define survey from ABMN locations
resistivity_survey = generate_survey_from_abmn_locations(
locations_a=locations_a,
locations_b=locations_b,
locations_m=locations_m,
locations_n=locations_n,
data_type="apparent_resistivity",
)
# Set geometric factor for survey (to be handled internally in future versions)
resistivity_survey.set_geometric_factor()array([-1.32679406e-03, -3.32234753e-04, -1.32564946e-04, -6.66158136e-05,
-3.81985175e-05, -2.39500693e-05, -1.59714066e-05, -1.21858389e-05,
-7.27199099e-06, -6.03996815e-06, -1.31970906e-03, -3.28433360e-04,
-1.32290024e-04, -6.62930265e-05, -3.80450422e-05, -2.37997557e-05,
-1.72442206e-05, -9.90213961e-06, -8.01655755e-06, -6.00391459e-06,
-1.31596261e-03, -3.31523324e-04, -1.32974869e-04, -6.66327740e-05,
-3.80450422e-05, -2.57898775e-05, -1.40852350e-05, -1.09570523e-05,
-7.95820474e-06, -5.96189404e-06, -1.32803712e-03, -3.33045228e-04,
-1.32974869e-04, -6.62930265e-05, -4.09920302e-05, -2.09533083e-05,
-1.54983451e-05, -1.08421814e-05, -7.88122772e-06, -5.81547319e-06,
-1.32803712e-03, -3.31523324e-04, -1.32290024e-04, -7.12317413e-05,
-3.32660994e-05, -2.32449626e-05, -1.55051270e-05, -1.08580263e-05,
-7.79793202e-06, -5.87960850e-06, -1.31596261e-03, -3.28433360e-04,
-1.40905176e-04, -5.74605436e-05, -3.68168421e-05, -2.30655327e-05,
-1.54030234e-05, -1.06450842e-05, -7.79793202e-06, -5.81547319e-06,
-1.31970906e-03, -3.50220207e-04, -1.14010065e-04, -6.48637549e-05,
-3.72019672e-05, -2.33071855e-05, -1.54030234e-05, -1.08580263e-05,
-7.88122772e-06, -5.96189404e-06, -1.37685904e-03, -2.78172165e-04,
-1.28908133e-04, -6.48637549e-05, -3.72019672e-05, -2.30655327e-05,
-1.55051270e-05, -1.08421814e-05, -7.95820474e-06, -6.00391459e-06,
-1.04059603e-03, -3.18025305e-04, -1.28908133e-04, -6.48637549e-05,
-3.68168421e-05, -2.32449626e-05, -1.54983451e-05, -1.09570523e-05,
-8.01655755e-06, -6.03996815e-06, -1.60461876e-03, -3.84828160e-04,
-1.51591590e-04, -7.47103667e-05, -4.27551299e-05, -2.66714770e-05,
-1.78398482e-05, -1.24935507e-05, -9.13176440e-06, -1.27020304e-03,
-3.12638682e-04, -1.23655353e-04, -6.17427108e-05, -3.52738615e-05,
-2.20352643e-05, -1.46528095e-05, -1.03260655e-05, -1.31970906e-03,
-3.28433360e-04, -1.32290024e-04, -6.62930265e-05, -3.80450422e-05,
-2.37997557e-05, -1.59714066e-05, -1.31596261e-03, -3.31523324e-04,
-1.32974869e-04, -6.66327740e-05, -3.80450422e-05, -2.39500693e-05,
-1.32803712e-03, -3.33045228e-04, -1.32974869e-04, -6.62930265e-05,
-3.81985175e-05, -1.32803712e-03, -3.31523324e-04, -1.32290024e-04,
-6.66158136e-05, -1.31596261e-03, -3.28433360e-04, -1.32564946e-04,
-1.31970906e-03, -3.32234753e-04, -1.32679406e-03])Define the Data¶
resistivity_data = data.Data(survey=resistivity_survey, dobs=apparent_resistivities)Assign Uncertainties¶
Uncertainties for apparent resistivity data were discussed earlier. Here we apply uncertainties of 1e-3 + 5 % to all data.
resistivity_data.standard_deviation = 1e-3 + 0.05 * np.abs(resistivity_data.dobs)Mapping from the Model to the Mesh¶
Here, the model defines the log-resistivity values for all active cells. We use the simpeg.maps.ExpMap to map from the model parameters to the resistivity values for all active cells. Then we use the simpeg
log_resistivity_map = maps.InjectActiveCells(mesh, active_cells, 1e8) * maps.ExpMap(
nP=n_active
)Starting/Reference Models¶
The starting model is defined according to the median apparent resistivity value. The reference model is equal to the starting model.
# Create starting model from log-resistivities
starting_resistivity_model = np.log(median_resistivity) * np.ones(n_active)
# Zero reference model
reference_resistivity_model = starting_resistivity_model.copy()Define the Forward Simulation¶
resistivity_simulation = dc.simulation_2d.Simulation2DNodal(
mesh, survey=resistivity_data.survey, rhoMap=log_resistivity_map, storeJ=True
)INFO: Setting the default solver 'Pardiso' for the 'Simulation2DNodal'.
To avoid receiving this message, pass a solver to the simulation. For example:
from simpeg.utils import get_default_solver
solver = get_default_solver()
simulation = Simulation2DNodal(solver=solver, ...)
Define the Data Misfit¶
dmis_irls = data_misfit.L2DataMisfit(
simulation=resistivity_simulation, data=resistivity_data
)Define the Regularization¶
Here, we use the Sparse regularization class to constrain the inversion result using an IRLS approach. Length scales along x and y are used to balance the smallness and smoothness terms. Here, length scales of 100 are used to more strongly emphasize smoothness in the recovered model. The reference model is only applied to the smallness term; which is redundant for the tutorial example since we have set the reference model to an array of zeros. Here, we apply a 0-norm to the smallness and 2-norm to first-order smoothness along the x and y directions.
reg_irls = regularization.Sparse(
mesh,
active_cells=active_cells,
length_scale_x=5.0,
length_scale_y=5.0,
norms=[0, 2, 2],
reference_model=reference_resistivity_model,
)Define the Optimization Algorithm¶
opt_irls = optimization.InexactGaussNewton(
maxIter=50, maxIterLS=20, cg_maxiter=20, cg_rtol=1e-3
)Define the Inverse Problem¶
inv_prob_irls = inverse_problem.BaseInvProblem(dmis_irls, reg_irls, opt_irls)Provide Inversion Directives¶
Here, we create common directives for IRLS inversion of total magnetic intensity data and describe their roles. In additon to the UpdateSensitivityWeights, UpdatePreconditioner and BetaEstimate_ByEig (described before), inversion with sparse-norms requires the UpdateIRLS directive.
You will notice that we don’t use the BetaSchedule and TargetMisfit directives. Here, the beta cooling schedule is set in the UpdateIRLS directive using the coolingFactor and coolingRate properties. The target misfit for the L2 portion of the IRLS approach is set with the chifact_start property.
sensitivity_weights_irls = directives.UpdateSensitivityWeights(
every_iteration=True, threshold_value=1e-2
)
update_irls = directives.UpdateIRLS(
cooling_factor=2,
cooling_rate=2,
f_min_change=1e-4,
max_irls_iterations=30,
chifact_start=1.0,
)
starting_beta_irls = directives.BetaEstimate_ByEig(beta0_ratio=10)
update_jacobi_irls = directives.UpdatePreconditioner(update_every_iteration=True)
directives_list_irls = [
update_irls,
sensitivity_weights_irls,
starting_beta_irls,
update_jacobi_irls,
]Define and Run the Inversion¶
inv_irls = inversion.BaseInversion(inv_prob_irls, directives_list_irls)
recovered_log_resistivity_model = inv_irls.run(starting_resistivity_model)
Running inversion with SimPEG v0.25.0
============================ Inexact Gauss Newton ============================
# beta phi_d phi_m f |proj(x-g)-x| LS Comment
-----------------------------------------------------------------------------
0 1.37e+00 4.48e+04 0.00e+00 4.48e+04
1 1.37e+00 2.06e+03 1.03e+03 3.47e+03 5.37e+03 0
2 1.37e+00 6.91e+02 1.71e+03 3.03e+03 4.37e+02 0
3 6.86e-01 3.42e+02 2.01e+03 1.72e+03 1.15e+02 0
4 6.86e-01 3.43e+02 1.97e+03 1.69e+03 1.06e+01 0
5 3.43e-01 1.99e+02 2.27e+03 9.76e+02 6.47e+01 0
6 3.43e-01 2.02e+02 2.23e+03 9.67e+02 5.17e+00 0
7 1.71e-01 1.36e+02 2.50e+03 5.65e+02 3.53e+01 0
8 1.71e-01 1.38e+02 2.46e+03 5.60e+02 3.43e+00 0
9 8.57e-02 1.06e+02 2.73e+03 3.40e+02 1.91e+01 0
Reached starting chifact with l2-norm regularization: Start IRLS steps...
irls_threshold 2.762186750761051
10 8.57e-02 1.11e+02 3.43e+03 4.06e+02 7.28e+00 0
11 1.38e-01 1.35e+02 3.30e+03 5.89e+02 1.71e+01 0
12 1.38e-01 1.35e+02 3.58e+03 6.28e+02 4.67e+00 0
13 1.38e-01 1.37e+02 3.60e+03 6.33e+02 1.76e+00 0
14 1.38e-01 1.38e+02 3.75e+03 6.54e+02 4.76e+00 0
15 1.38e-01 1.39e+02 3.78e+03 6.60e+02 1.84e+00 0
16 1.38e-01 1.39e+02 3.87e+03 6.72e+02 5.25e+00 0
17 1.38e-01 1.41e+02 3.90e+03 6.78e+02 1.96e+00 0
18 1.38e-01 1.41e+02 3.93e+03 6.81e+02 5.74e+00 0
19 1.38e-01 1.43e+02 3.95e+03 6.87e+02 1.87e+00 0
20 1.38e-01 1.42e+02 3.93e+03 6.83e+02 6.11e+00 0
21 1.38e-01 1.44e+02 3.94e+03 6.86e+02 1.68e+00 0
22 1.38e-01 1.42e+02 3.87e+03 6.75e+02 6.38e+00 0
23 1.38e-01 1.45e+02 3.87e+03 6.77e+02 1.57e+00 0
24 1.38e-01 1.42e+02 3.77e+03 6.61e+02 6.62e+00 0
25 1.38e-01 1.45e+02 3.75e+03 6.61e+02 1.50e+00 0
26 1.38e-01 1.42e+02 3.62e+03 6.41e+02 6.83e+00 0
27 1.38e-01 1.44e+02 3.60e+03 6.40e+02 1.39e+00 0
28 1.38e-01 1.42e+02 3.46e+03 6.17e+02 7.01e+00 0
29 1.38e-01 1.44e+02 3.43e+03 6.16e+02 1.22e+00 0
30 1.38e-01 1.41e+02 3.28e+03 5.92e+02 7.12e+00 0
31 1.38e-01 1.43e+02 3.26e+03 5.91e+02 1.01e+00 0
32 1.38e-01 1.41e+02 3.10e+03 5.68e+02 7.17e+00 0
33 1.38e-01 1.42e+02 3.08e+03 5.66e+02 8.17e-01 0
34 1.38e-01 1.41e+02 2.93e+03 5.44e+02 7.17e+00 0
35 1.38e-01 1.42e+02 2.91e+03 5.42e+02 6.66e-01 0
36 1.38e-01 1.41e+02 2.76e+03 5.21e+02 7.25e+00 0
37 1.38e-01 1.41e+02 2.75e+03 5.20e+02 5.67e-01 0
38 1.38e-01 1.40e+02 2.62e+03 5.01e+02 7.58e+00 0
39 1.38e-01 1.41e+02 2.61e+03 5.00e+02 5.09e-01 0
40 1.38e-01 1.40e+02 2.48e+03 4.82e+02 7.84e+00 0
41 1.38e-01 1.40e+02 2.47e+03 4.80e+02 4.82e-01 0
42 1.38e-01 1.39e+02 2.35e+03 4.62e+02 8.37e+00 0
43 1.38e-01 1.39e+02 2.34e+03 4.61e+02 4.78e-01 0
44 1.38e-01 1.37e+02 2.22e+03 4.43e+02 8.94e+00 0
45 1.38e-01 1.37e+02 2.22e+03 4.42e+02 4.84e-01 0
46 1.38e-01 1.36e+02 2.10e+03 4.25e+02 9.16e+00 0
47 1.38e-01 1.36e+02 2.10e+03 4.24e+02 4.71e-01 0
48 1.38e-01 1.35e+02 1.99e+03 4.09e+02 8.98e+00 0
49 1.38e-01 1.35e+02 1.99e+03 4.08e+02 4.29e-01 0
50 1.38e-01 1.34e+02 1.89e+03 3.95e+02 8.59e+00 0
------------------------- STOP! -------------------------
1 : |fc-fOld| = 1.4951e+00 <= tolF*(1+|f0|) = 4.4850e+03
1 : |xc-x_last| = 7.2204e-01 <= tolX*(1+|x0|) = 3.8989e+01
0 : |proj(x-g)-x| = 3.7762e-01 <= tolG = 1.0000e-01
0 : |proj(x-g)-x| = 3.7762e-01 <= 1e3*eps = 1.0000e-02
1 : maxIter = 50 <= iter = 50
------------------------- DONE! -------------------------
Plot True, L2 and IRLS Models¶
Here, we compare the models recovered from weighted least-squares and iteratively re-weighted least-squares inversion to the true model.
# Recreate the true model
true_background_conductivity = 1e-2
true_conductor_conductivity = 1e-1
true_resistor_conductivity = 1e-3
true_conductivity_model = true_background_conductivity * np.ones(n_active)
ind_conductor = model_builder.get_indices_sphere(
np.r_[-120.0, 40.0], 60.0, mesh.cell_centers[active_cells, :]
)
true_conductivity_model[ind_conductor] = true_conductor_conductivity
ind_resistor = model_builder.get_indices_sphere(
np.r_[120.0, 72.0], 60.0, mesh.cell_centers[active_cells, :]
)
true_conductivity_model[ind_resistor] = true_resistor_conductivity# Convert recovered log-resistivities to conductivities
recovered_conductivity_irls = 1 / np.exp(recovered_log_resistivity_model)# Convert to subsurface conductivity values
plotting_model = [
true_conductivity_model,
recovered_conductivity_L2,
recovered_conductivity_irls,
]
fig = plt.figure(figsize=(9, 13))
ax1 = 3 * [None]
ax2 = 3 * [None]
title_str = [
"True Conductivity Model",
"Recovered Model (L2)",
"Recovered Model (IRLS)",
]
for ii in range(0, 3):
ax1[ii] = fig.add_axes([0.14, 0.75 - 0.3 * ii, 0.68, 0.22])
mesh.plot_image(
plotting_map * plotting_model[ii],
ax=ax1[ii],
grid=False,
pcolor_opts={"norm": norm, "cmap": mpl.cm.RdYlBu_r},
)
ax1[ii].set_xlim(-500, 500)
ax1[ii].set_ylim(-300, 200)
ax1[ii].set_title(title_str[ii])
ax1[ii].set_xlabel("x (m)")
ax1[ii].set_ylabel("z (m)")
ax2[ii] = fig.add_axes([0.84, 0.75 - 0.3 * ii, 0.03, 0.22])
cbar = mpl.colorbar.ColorbarBase(
ax2[ii], norm=norm, orientation="vertical", cmap=mpl.cm.RdYlBu_r
)
cbar.set_label(r"$\sigma$ (S/m)", rotation=270, labelpad=15, size=12)
plt.show()