Reproduce: SimPEG OcTree#
Simulating Pole-Dipole DC Resistivity Data over a Conductive and a Resistive Block#
Pole-dipole DC resistivity data are simulated over both a conductive and a resistive block. The background conductivity is \(\sigma_0\) = 0.01 S/m. The conductor has a conductivity of \(\sigma_c\) = 0.1 S/m and the resistor has a conductivity of \(\sigma_r\) = 0.001 S/m. Both blocks are oriented along the Northing direction and have x, y and z dimensions of 400 m, 800 m and 320 m. Both blocks are buried at a depth of 160 m.
DC voltage data are simulated with a pole-dipole configuration. The survey consists of 9 West-East survey lines, each with a length of 2000 m. The line spacing is 250 m and the electrode spacing is 100 m.
SimPEG Package Details¶#
Link to the docstrings for the simulation class.
Running the Forward Simulation#
We begin by loading all necessary packages and setting any global parameters for the notebook.
Show code cell source
from SimPEG import dask
from SimPEG.electromagnetics.static import resistivity as dc
from SimPEG.electromagnetics.static.utils.static_utils import plot_3d_pseudosection, apparent_resistivity
from SimPEG.utils.io_utils import read_dcipoctree_ubc, write_dcipoctree_ubc
from SimPEG import maps, data
from discretize import TreeMesh
import matplotlib as mpl
import matplotlib.pyplot as plt
import plotly
import numpy as np
from pymatsolver import Pardiso
mpl.rcParams.update({"font.size": 14})
write_output = True
A compressed folder containing the assets required to run the notebook is then downloaded. This includes mesh, model and survey files for the forward simulation.
Show code cell source
# Download .tar
Extracted files are then loaded into the SimPEG framework.
Show code cell source
rootdir = './../../../assets/dcip/block_model_dc_fwd_simpeg_octree/'
meshfile = rootdir + 'octree_mesh.txt'
confile = rootdir + 'true_model.con'
locfile = rootdir + 'survey.loc'
mesh = TreeMesh.readUBC(meshfile)
conductivity_model = TreeMesh.readModelUBC(mesh, confile)
dc_data = read_dcipoctree_ubc(locfile, 'volt')
Below, we plot the model and the survey geometry used in the forward simulation.
Show code cell source
vmin = np.log10(conductivity_model.min())
vmax = np.log10(conductivity_model.max())
ind = int(len(mesh.hy)/2)
fig = plt.figure(figsize=(15, 3.5))
ax1 = fig.add_axes([0.1, 0.12, 0.4, 0.78])
mesh.plotSlice(
np.log10(conductivity_model), ax=ax1, normal='Y', grid=True,
ind=ind, clim=(vmin, vmax), pcolorOpts={"cmap": "viridis"},
)
ax1.set_title("Conductivity Model")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("z (m)")
ax2 = fig.add_axes([0.51, 0.12, 0.015, 0.78])
norm = mpl.colors.Normalize(
vmin=vmin, vmax=vmax
)
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, cmap=mpl.cm.viridis, orientation="vertical", format="$10^{%.1f}$"
)
cbar.set_label("Conductivity [S/m]", rotation=270, labelpad=15, size=12)
ax3 = fig.add_axes([0.7, 0.12, 0.2, 0.78])
ind = int(len(mesh.hz)-10)
masked_model = np.log10(conductivity_model)
masked_model[masked_model==-2]=np.NaN
mesh.plot_slice(
masked_model, ax=ax3, normal='Z', grid=True,
ind=ind, clim=(vmin, vmax), pcolorOpts={"cmap": "viridis"},
)
for ii in range(0, 9):
ax3.plot(np.arange(-1000, 1000, 100), -1000+ii*250*np.ones(20), 'ro', markersize=4)
ax3.set_xlim([-1100, 1100])
ax3.set_ylim([-1100, 1100])
ax3.set_xlabel('x (m)')
ax3.set_ylabel('y (m)')
ax3.set_title('Survey Geometry')
Text(0.5, 1.0, 'Survey Geometry')
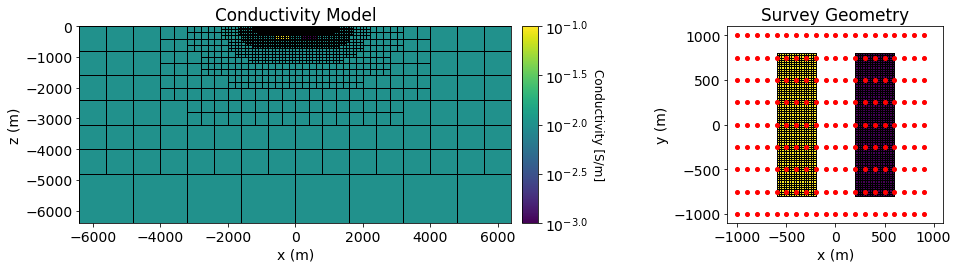
Here we define the mapping from the model to the mesh, extract the survey from the data object and define the forward simulation.
Show code cell source
model_map = maps.IdentityMap(nP=mesh.nC)
dc_survey = dc_data.survey
dc_simulation = dc.simulation.Simulation3DNodal(
mesh, survey=dc_survey, sigmaMap=model_map,
solver=Pardiso, verbose=True, bc_type='Neumann'
)
Homogeneous Neumann is the natural BC for this nodal discretization.
Finally, we predict DC data for the model provided.
Show code cell source
dpred_simpeg = dc_simulation.dpred(conductivity_model)
If desired, we can export the simulated DC resistivity data to a UBC formatted data file.
Show code cell source
if write_output:
data_simpeg = data.Data(survey=dc_survey, dobs=dpred_simpeg)
outname = rootdir + 'dpred_simpeg.txt'
write_dcipoctree_ubc(outname, data_simpeg, 'volt', 'dpred')
np.random.seed(83)
standard_deviation = 1e-6 + 0.05*np.abs(dpred_simpeg)
dobs = dpred_simpeg + standard_deviation * np.random.rand(len(standard_deviation))
dobs_simpeg = data.Data(survey=dc_survey, dobs=dobs, standard_deviation=standard_deviation)
outname = rootdir + 'dobs_simpeg.txt'
write_dcipoctree_ubc(outname, dobs_simpeg, 'volt', 'dobs')
Plotting Simulated Voltage Data#
Show code cell source
mpl.rcParams.update({'font.size': 16})
plane_points = []
for x in np.arange(-1000, 1100, 500):
p1, p2, p3 = np.array([-1000.,x,0]), np.array([1000,x,0]), np.array([1000,x,-1000])
plane_points.append([p1,p2,p3])
scene_camera=dict(
center=dict(x=-0.05, y=0, z=-0.2), eye=dict(x=1.1, y=-0.9, z=1.35)
)
scene = dict(
xaxis=dict(range=[-1000, 1000]), yaxis=dict(range=[-1000, 1000]),
zaxis=dict(range=[-500, 0]), aspectratio=dict(x=1, y=1, z=0.5)
)
vlim = [dpred_simpeg.min(), dpred_simpeg.max()]
fig1 = plot_3d_pseudosection(
dc_survey, dpred_simpeg, scale='log', vlim=vlim,
plane_points=plane_points, plane_distance=10., units='V'
)
fig1.update_layout(
title_text="Voltage Data", title_x=0.5, width=800, height=700,
scene_camera=scene_camera, scene=scene
)
plotly.io.show(fig1)
Plot as Apparent Conductivities#
Show code cell source
mpl.rcParams.update({'font.size': 16})
app_cond = 1./apparent_resistivity(
dc_data, space_type="half space", dobs=dpred_simpeg, eps=1e-10,
)
plane_points = []
for x in np.arange(-1000, 1100, 500):
p1, p2, p3 = np.array([-1000.,x,0]), np.array([1000,x,0]), np.array([1000,x,-1000])
plane_points.append([p1,p2,p3])
vlim = [app_cond.min(), app_cond.max()]
fig1 = plot_3d_pseudosection(
dc_survey, app_cond, scale='log', vlim=vlim,
plane_points=plane_points, plane_distance=10., units='S/m'
)
fig1.update_layout(
title_text="Apparent Conductivities", title_x=0.5, width=800, height=700,
scene_camera=scene_camera, scene=scene
)
plotly.io.show(fig1)
