Reproduce: Analytic#
Simulating Secondary Magnetic Field Data over a Conductive Sphere#
Secondary magnetic fields are simulated over conductive sphere in a vacuum. The sphere has a conductivity of \(\sigma\) = 1 S/m. The center of the sphere is located at (0,0,-50) and has a radius of \(a\) = 8 m.
Secondary magnetic fields are simulated for an x, y and z oriented magnetic dipoles sources at (-5,0,10). The x, y and z components of the response are simulated for each source at (5,0,10). We plot only the horizontal coaxial, horizontal coplanar and vertical coplanar data.
Package Details#
Wait and Spies analytic solution. See https://em.geosci.xyz/content/maxwell3_fdem/inductive_sources/sphere/index.html for a summary of the solution.
Reference: J. R. Wait. A conductive sphere in a time varying magnetic field. Geophysics, 16:666–672, 1951.
Reproducing the Forward Simulation Result#
We begin by loading all necessary packages and setting any global parameters for the notebook.
Show code cell source
from SimPEG.utils import mkvc
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams.update({"font.size": 10})
write_output = True
Here we define the sphere model.
Show code cell source
rootdir = './../../../assets/fdem/sphere_vacuum_conductive_fwd_simpeg/'
a = 8 # radius of sphere
sig0 = 1e-8 # background conductivity
sig = 1e0 # electrical conductivity of sphere
chi = 0. # relative permeability of sphere
xyzs = [0., 0., -50.] # xyz location of the sphere
mur = 1 + chi
Here, we define the survey geometry for the forward simulation.
Show code cell source
xyz_tx = np.c_[-5., 0., 10.] # Transmitter location
xyz_rx = np.c_[5., 0., 10.] # Receiver location
frequencies = np.logspace(2,5,10) # Frequencies
tx_moment = 1. # Dipole moment of the transmitter
Here we define some functions that are used to compute the analytic forward solution.
Show code cell source
def compute_primary_field_dipole(orientation, pxyz, qxyz):
"""
For an X, Y or Z orientationed magnetic dipole, compute the free-space primary field for a dipole moment of 1.
orientation: 'x', 'y' or 'z'
pxyz : [x,y,z] locations of the dipole transmitters
qxyz : [x,y,z] location at the centre location of the sphere
"""
R = np.sqrt((qxyz[0] - pxyz[:,0]) ** 2 + (qxyz[1] - pxyz[:,1]) ** 2 + (qxyz[2] - pxyz[:,2]) ** 2)
if orientation == "x":
Hpx = (1 / (4 * np.pi)) * (3 * (qxyz[0] - pxyz[:,0]) * (qxyz[0] - pxyz[:,0]) / R ** 5 - 1 / R ** 3)
Hpy = (1 / (4 * np.pi)) * (3 * (qxyz[1] - pxyz[:,1]) * (qxyz[0] - pxyz[:,0]) / R ** 5)
Hpz = (1 / (4 * np.pi)) * (3 * (qxyz[2] - pxyz[:,2]) * (qxyz[0] - pxyz[:,0]) / R ** 5)
elif orientation == "y":
Hpx = (1 / (4 * np.pi)) * (3 * (qxyz[0] - pxyz[:,0]) * (qxyz[1] - pxyz[:,1]) / R ** 5)
Hpy = (1 / (4 * np.pi)) * (3 * (qxyz[1] - pxyz[:,1]) * (qxyz[1] - pxyz[:,1]) / R ** 5 - 1 / R ** 3)
Hpz = (1 / (4 * np.pi)) * (3 * (qxyz[2] - pxyz[:,2]) * (qxyz[1] - pxyz[:,1]) / R ** 5)
elif orientation == "z":
Hpx = (1 / (4 * np.pi)) * (3 * (qxyz[0] - pxyz[:,0]) * (qxyz[2] - pxyz[:,2]) / R ** 5)
Hpy = (1 / (4 * np.pi)) * (3 * (qxyz[1] - pxyz[:,1]) * (qxyz[2] - pxyz[:,2]) / R ** 5)
Hpz = (1 / (4 * np.pi)) * (3 * (qxyz[2] - pxyz[:,2]) * (qxyz[2] - pxyz[:,2]) / R ** 5 - 1 / R ** 3)
return np.c_[Hpx, Hpy, Hpz]
def compute_excitation_factor(f, sig, mur, a):
"""
Compute Excitation Factor (FEM)
f : frequencies
sig : conductivity
mur : relative permeability
a : radius
"""
w = 2 * np.pi * f
mu = 4 * np.pi * 1e-7 * mur
alpha = a * np.sqrt(1j * w * mu * sig)
chi = (
1.5
* (
2 * mur * (np.tanh(alpha) - alpha)
+ (alpha ** 2 * np.tanh(alpha) - alpha + np.tanh(alpha))
)
/ (
mur * (np.tanh(alpha) - alpha)
- (alpha ** 2 * np.tanh(alpha) - alpha + np.tanh(alpha))
)
)
return chi
def compute_dipolar_response(m, pxyz, qxyz):
"""
For a sphere with dipole moment [mx, my, mz], compute the dipolar response
m : dipole moments [mx, my, mz]
orientation of the receiver: 'x', 'y' or 'z'
pxyz : [x,y,z] locations of the receivers
qxyz : [x,y,z] location at the centre location of the sphere
"""
R = np.sqrt((qxyz[0] - pxyz[:,0]) ** 2 + (qxyz[1] - pxyz[:,1]) ** 2 + (qxyz[2] - pxyz[:,2]) ** 2)
Hx = (1 / (4 * np.pi)) * ( 3 * (pxyz[:,0] - qxyz[0]) * (
m[:,0]*(pxyz[:,0] - qxyz[0]) +
m[:,1]*(pxyz[:,1] - qxyz[1]) +
m[:,2]*(pxyz[:,2] - qxyz[2])
) / R ** 5 - m[:,0] / R ** 3)
Hy = (1 / (4 * np.pi)) * ( 3 * (pxyz[:,1] - qxyz[1]) * (
m[:,0]*(pxyz[:,0] - qxyz[0]) +
m[:,1]*(pxyz[:,1] - qxyz[1]) +
m[:,2]*(pxyz[:,2] - qxyz[2])
) / R ** 5 - m[:,1] / R ** 3)
Hz = (1 / (4 * np.pi)) * ( 3 * (pxyz[:,2] - qxyz[2]) * (
m[:,0]*(pxyz[:,0] - qxyz[0]) +
m[:,1]*(pxyz[:,1] - qxyz[1]) +
m[:,2]*(pxyz[:,2] - qxyz[2])
) / R ** 5 - m[:,2] / R ** 3)
return np.c_[Hx, Hy, Hz]
Finally, we predict the secondary magnetic field data for the model provided.
Show code cell source
Hs_analytic = []
for ii, comp in enumerate(['x','y','z']):
# Compute the free space primary field at the location of the sphere
Hp = tx_moment*compute_primary_field_dipole(comp, xyz_tx, xyzs)
temp = []
for jj in range(0, len(frequencies)):
# Multiply by the excitation factor to get the dipole moment of the sphere
m = (4*np.pi*a**3/3)*compute_excitation_factor(frequencies[jj], sig, mur, a) * Hp
# Compute dipolar response
temp.append(compute_dipolar_response(m, xyz_rx, xyzs))
Hs_analytic.append(np.vstack(temp))
We can export the data to a simple text file.
Show code cell source
if write_output:
fname_analytic = rootdir + 'analytic.txt'
header = 'FREQUENCY HX_REAL HX_IMAG HY_REAL HY_IMAG HZ_REAL HZ_IMAG'
f_column = np.kron(np.ones(3), frequencies)
out_array = np.vstack(Hs_analytic)
out_array = np.c_[
f_column,
np.real(out_array[:, 0]),
np.imag(out_array[:, 0]),
np.real(out_array[:, 1]),
np.imag(out_array[:, 1]),
np.real(out_array[:, 2]),
np.imag(out_array[:, 2])
]
fid = open(fname_analytic, 'w')
np.savetxt(fid, out_array, fmt='%.6e', delimiter=' ', header=header)
fid.close()
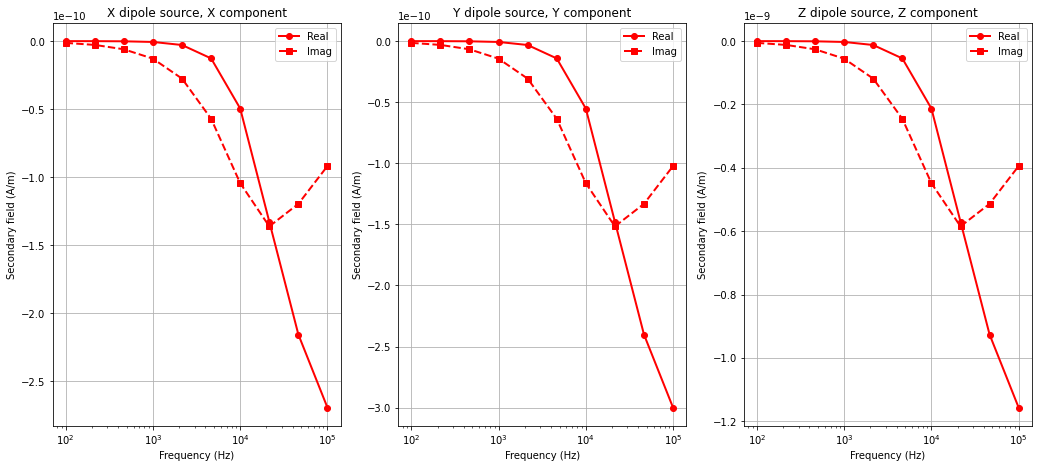
Simulated Data Plot#
Show code cell source
fig = plt.figure(figsize=(16, 7))
lw = 2
ms = 6
ax = 3*[None]
legend_str = ['Real', 'Imag']
for ii, src in enumerate(['X','Y','Z']):
ax[ii] = fig.add_axes([0.05 + 0.3*ii, 0.1, 0.25, 0.8])
ax[ii].semilogx(frequencies, np.real(Hs_analytic[ii][:, ii]), 'r-o', lw=lw, markersize=ms)
ax[ii].semilogx(frequencies, np.imag(Hs_analytic[ii][:, ii]), 'r--s', lw=lw, markersize=ms)
ax[ii].grid()
ax[ii].set_xlabel('Frequency (Hz)')
ax[ii].set_ylabel('Secondary field (A/m)')
ax[ii].set_title(src + ' dipole source, ' + src + ' component')
ax[ii].legend(legend_str)